ARIMA모형을 이용한 한국 아동·청소년의 체격과 BMI 장기 예측
Chae, Jin-Seok1*; Song, Jong-Kook2
체육과학연구Korean Journal of Sport Science, Vol.27, No.3, pp.530-542
Abstract
The present study has been carried out with a purpose of a long term estimation for the body size and BMI (Body Mass Index) of Korean children and youth using ARIMA, a time series model. In order to select an estimation model for the optimum time series, among the time series analysis method of SPSS22.0 statistic programs, a multivariate ARIMA (p,d,q) model has been selected that has an input series (physical education facility, time spent for physical education, animal source foods, GDP deflator, animal source food intake ratio), using annual average data of height, weight, and BMI data from 1965 to 2015. Among the several optimal measurements in ARIMA model with estimation variables, an optimal RMSE-based model (RMSE: Root Mean Square Error) has been selected. Using this model, the estimation model and estimated values of children’s height, weight, and BMI have been suggested for each age group. The results are as the following. The trend estimation of height follows a logistic curve, with both male and female groups showing increasing trends. The weight has a trend of increasing ratio higher than height. BMI also shows a trend curve similar to weight. The estimation model has been mostly ARIMA(0,1,0). In particular, the average BMI has been estimated as 22-23 for male students in 6th, 8th, 9th, 11th and 12th grade in 2030. This indicates the recent increasing obesity as children and youth occupy most of daily time for play culture that is far from physical activities, such as computer games, smartphone games, and video games at home.
초록
본 연구는 시계열모형인 ARIMA모형을 이용하여 아동·청소년의 체격과 BMI를 장기 예측하는 것을 목적으로 수행되었다. 최적의 시계열 예측모형을 선택하기위해 1965년부터 2015년까지의 연간평균자료인 키, 몸무게, BMI자료를 이용하여 SPSS22.0 통계프로그램의 시계열분석방법 중 입력계열(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)이 있는 다변량ARIMA(p,d,q)모형을 선택하였다. 예측변인이 있는 ARIMA모형에서 여러 가지 적합도 측도 중 제곱근평균제곱오차(RMSE)를 고려한 최적의 모형을 선택하도록 하였다. 이 모형을 적용하여 아동·청소년의 키, 몸무게, BMI의 예측모형과 예측값을 나이 별로 제시하였다. 결론은 다음과 같다. 키의 예측추세 특징은 남·여 모두 증가추세로 로지스틱 곡선을 따르고 있었다. 체중은 키보다는 증가율이 높은 추세가 있었으며, BMI도 체중과 비슷한 추세곡선을 나타내고 있었다. 예측모형은 대부분 ARIMA(0,1,0)모형 이였고 특히 2030년의 초6, 중2, 중3, 고2, 고3 남학생의 평균 BMI가 22-23이상을 예측한 것은 최근 아동·청소년들의 집에서 컴퓨터게임, 핸드폰 게임, 오락기기게임 등 신체활동과 거리가 먼 놀이문화로 이들의 하루시간을 대부분 차지하고 있는 현실에서 비만의 증가를 대변하고 있다.
서 론
교육부에서 매년 실시하는 아동·청소년의 체격·체력검사 자료는 1965년부터 제공하고 있다. 이 자료를 살펴보면 아동·청소년들의 체격과 체력이 과거 51년에 비해 변화가 크다. 체격은 커져 가는데 체력은 떨어지는 역 현상이 나타나고 있다. 선진국에서는 국가적 차원에서 국민건강과 체력향상을 위해 사회체육정책을 수립하고 학교체육의 활성화를 위해 클럽활동을 강화하고 있다(Shephard, 1997; Kirby et al., 2012; The Ministry of Education, Science and Technology, 2012). 형태는 다르지만 1970대 한국도 대학입시전형에 체력장 검사점수가 반영되는 연유로 학생들의 체력이 향상된 시기가 있었다. 그러나 체육을 소홀이하고 국·영·수 과목을 위주로 교육하는 입시체계와 문명의 발달로 학생들의 체육수업시간을 줄어드는 것과 동시에 컴퓨터 게임, TV시청, 핸드폰 게임 등의 시간이 증가로 아동·청소년들의 신체활동 저하로 인한 체력 감소는 사회적 이슈가 되고 있다(Young et al., 2007; Yeun, 2012; Kim & Kim, 2013; Chae & Shin, 2015).
이러한 현상을 완화해보고자 2013년 1월 27일 국가는 학교체육진흥법을 제정하여 매년 학생건강 체력을 평가하고 저체력 또는 비만학생을 위한 건강체력 교실을 운영할 의무를 다하고 있다. 현재 신체활동부족의 산물인 비만과 대사증후군은 전 세계적으로도 급속히 늘고 있으며(Twisk et al., 2002), 국내만 하더라도 매년 약 40만 명의 성인 비만 환자가 늘고 있다(보건복지부, 2013). 국민건강통계에 따르면 비만 유병률은 1998년 26.0%에서 2011년 31.4%로 증가 추이를 보이며, 남자 35.1%, 여자 27.1%로 남자가 여자보다 8%정도 높다(Centers for Disease Control and Prevention, 2013). 이러한 비만 유병률의 증가 속에서 아동·청소년의 체격·체력의 예측은 학생들과 학부모를 비롯한 국가에게 체격·체력에 대한 중요성을 인식시키고 체격·체력 증진에 대한 관심을 유도하는 기능이 있다. 또한 이들 청소년들이 성장하여 국가의 중추기관을 맡을 인재인 만큼 이들의 체격과 신체조성 및 체력이 어떻게 변화해 갈 것인가를 예측하는 일은 매우 중요하리라 여겨진다.
또한 체격은 국력으로 나타내는 한지표이다. 국력의 가장 원시적인 요소로는 인구·영토·천연자원의 3가지를 들 수 있다. 이중에서 체격은 인구에 해당된다. 체격의 평가는 신장·체중·가슴둘레·앉은키 등 신체계측 값 및 이들의 상호작용에 의해서 이루어진다. 이 상호작용의 하나인 신체질량 지수(BMI:Body mass index)는 체중과 신장의 비율로 계산되며, 비만의 정도를 알 수 있게 제안된 지수이다. 이 처럼 체격과 BMI는 국가의 힘과 국민의 건강을 알 수 있는 요소이므로 이들의 미래를 예측하는 것은 필요충분하다고 생각된다.
최근 신문지상에 인천공항에서 하루 동안 출발, 도착 지연이 무려 160여 편이 생겨 라는 제목의 기사가 작성되었다. 이 기사는 ʻʻ공항이용객이 매년 10%씩 빠르게 증가했다ʼʼ 면서 인천공항 터미널이 2015년 이미 포화 상태에 이른다는 사실이 이미 오래전에 예고됐던 점에 비춰 볼 때 확장공사를 제 때에 예측 못해 실기한 측면이 있다고 말했다(Chosun newspaper, 2016). 이렇듯 수요예측의 실패는 물론이고 가뭄과 홍수, 지진 등 천재지변을 정확히 예측을 못하여 수많은 인명피해가 발생 하는 장면을 뉴스에서 우리는 종종보고 있다.
얼마 전 뉴욕 타임스가 보도한 이 사례는 예측의 효과를 잘 보여주었다. 대형마트는 미성년 여자에게 임신에 필요한 물건의 쿠폰을 보내주었고 그것을 본 아버지의 항의를 받았다. 그러나 뒤늦게 딸아이가 임신한 사실을 알고는 마트에 사과했다는 기사이다. 미성년 딸이 부모 모르게 아이를 가졌던 것이다. 부모도 모르는 딸의 임신, 대형마트는 알고 있었다. 대형마트 마케팅팀은 부모도 몰랐던 딸의 임신 사실을 어떻게 알아챘을까? 답은 ‘빅데이터 분석’에 있었다. 이 얘기는 미국 대형마트 ‘타깃’의 미니애폴리스 점포에서 실제로 일어났던 일이다. 타깃의 빅데이터 전문가들은 고객의 25가지 구매 행태를 분석하면 여성의 임신과 출산을 상당히 정확하게 예측할 수 있다는 사실을 확인했다(Hankyoreh newspaper, 2016).
이처럼 빅데이터의 힘은 정보 수집과 분석을 통한 ‘미래 예측’에서 나온다. 미래에 발생할 사건의 결과는 현재의 의사결정에 매우 중요한 역할을 하기 때문에 앞으로의 계획을 합리적으로 설계하고 이에 따른 손실을 가능한 축소하기 위해서는 미래에 대한 정확한 예측이 필요하다. 이미 미래예측 활동이 활발하게 이루어지고 있는 선진국들의 경우, 단순 추세분석에서부터 국가 전략기획 수립에 이르기까지 각 분야에 맞는 다양한 운용방법을 활용하고 있다고 하며, 국내·외 전자 데이터베이스를 이용하여, 논문명, 키워드, 초록에 예측과 관련된 ‘시계열 분석’을 조사한 결과 6,543건 문헌 중에서 1987년부터 2013년까지 시계열 분석을 활용한 논문은 점차 증가하고 있는 추세였다(Lee & Kim, 2015).
또한 스포츠분야에서 예측과 관련된 연구는 인공신경망을 이용한 축구·야구·테니스경기 승·패 예측모형 개발(Kim et al., 2007; Choi & Kim, 2006; Chae et al., 2010; Chae & Song, 2014)과 프로 야구와 축구의 관중수 예측과 골프 내장객 수요예측 및 스포츠 센타 수요예측 그리고 경마 매출액 예측 연구 등이 주를 이루고 있었다(Stefani, 2003; Kim, 2009; Sul et al., 2011; Choi & Jeong, 2010; Sul et al., 2011; Chae, 2012; Kim & Chae, 2012; Han & Kim, 2013; Choi & Kim, 2013; Yoon & Ahn, 2013).
이들 논문의 분석기법은 지수평활모형(단순, Holt, Brown, 진폭감소 추세)과 ARIMA모형, 시계열 회귀모형 등을 사용하였으며, 시도된 예측에 관한 시계열분석 논문은 크게 두 가지 형태로 나눌 수 있었다. 하나는 예측변수가 적용이 안 된 단변량 시계열분석방법과 예측변수가 적용된 다변량 시계열분석방법으로 구분 할 수 있었으며 다변량 시계열분석방법 보다는 단변량 시계열분석방법이 더 많았다.
또한 스포츠분야외의 다양한 학문인 인문학, 자연과학, 공학, 의약학, 농수해양, 복합학에서도 시계열분석방법이 활용이 높았다. 특히 수요예측을 다루는 타 학문분야인 산업공학, 관광, 경제, 경영, 의료, 지질, 기후, 보험, 금융 등에서는 시계열분석 예측논문이 활발하게 생산되고 있는 실정으로 실업률, 국내총생산량, GNP, 물가지수, 주가지수, 총 수출액, 판매량, 광고액, 재고량, 고객수, 교통량, 의존주의보 날짜, 대기오염, 신호처리, 지진파, 소매치 건수, 일별 맥박 수, 혈압, 연도별 태양의 흑점 수, 별의 밝기, 탄약수명, 미래소득, 게임 접속시간, 환율동향, 수문량, 지하수관측, 소프트웨어 미래 고장시간, 해안의 용존산소량, 진료자료의 재고량수요, 연도별 이민자수, 항공 기내식 수요, 정책단절, 통합공정관리, 국제유가, 아파트 전·월세 수요, 관광객 수요, 패션산업 인력수요, 차세대에너지구축을 위한 도시기상조건 등 다양한 분야의 시계열 자료를 이용, 예측성과를 보여주고 있었다.
이들 논문의 주요 분석 기법은 ARIMA 모형, 시계열 회귀모형 순으로 활용되었고 자료의 대부분은 통계청과 정부기관에서 생산하는 통계자료이며, 시간과 더불어 관측된 자료로 이는 종단면 자료(longitudinal data)에 해당 한다(Woo & Shin, 2014). 본 연구 자료도 시간에 따라 연도별로 나타낸 종단면 자료로 정부기관인 교육부자료를 이용하였다. 연구 변인의 특징을 살펴보면 종속변수인 키, 체중, BMI를 잘 설명하고 예측할 수 있도록 도와주는 독립변수로 체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율이 선택되었다. 이는 체육시설인 학교 실내·외 운동장의 면적의 감소와 체육시간의 감소는 연구대상자들의 신체활동을 제한 할 것으로 예상되며, 종속변수인 키, 체중, BMI에 영향을 줄 것으로 예견된다.
산업자원부 기술표준원의 조사에 따르면, 한국인의 체격은 영양상태의 개선과 생활양식의 변화 등의 사회경제적 요인의 변화에 따라 점차 서구화되는 경향을 띠며, 한국인의 체형은 예전보다 키는 커지고 얼굴은 작아지는 경향을 보인다(산업자원부 기술표준원, 2007).고 제시한 연구보고서는 본 연구의 설명변수로 동물성식품, GDP디플레이터, 동물성식품섭취분율을 선택하게 한 이론적 배경이라 할 수 있다.
이러한 독립·종속시계열자료는 어떠한 경제 현상이나 자연 현상에 관한 시간적 변화를 나타내는 자료이므로 어느 한 시점에서 관측된 시계열 자료는 그 이전까지의 자료들에 의존하게 된다. 시계열분석(時系列分析, time series analysis)을 통한 예측에서는 관측된 과거의 자료들을 분석하여 이를 모형화하고, 이 추정된 모형을 사용하여 미래에 관측될 값들을 정확하게 예측할 필요성이 있다.
이상 선행연구와 필요성을 살펴본바 시계열자료인 체격과 신체조성의 움직임을 설명하는 예측모형의 수립(model building)을 위해 1965년부터 2015년까지의 연간평균자료인 키, 몸무게, BMI자료를 이용, 시계열분석 방법으로 자주 사용되어온 자기회귀통합이동평균ARIMA(p,d,q)모형을 토대로 예측 값을 최종 나이 별로 제시함으로서 국가정책의 의사결정 해결 자료로 쓰이는 것이 본 연구의 목적이다.
연구방법
연구대상 및 자료수집
본 연구에서 사용된 자료의 범위는 아동·청소년(6살-17살)의 키, 몸무게로 1965년부터 2015년까지의 평균자료이며, 연도별, 연령별, 성별로 구분한 표본 수는 약 1,000명~4,900명으로 각각 다르게 수집 적용되었다. 시계열분석을 위해 연도별, 성별, 연령별, 체격자료를 Microsoft사의 Excel 2007 프로그램을 사용하여 정리한 후 SPSS통계프로그램에 코딩하였다. 또한 신장과 체중 자료를 활용하여 신체조성 변수인 체질량지수(Body Mass Index, BMI, kg/㎡)를 산출하였다.
각 표본 측정값은 남·여 각각 6살(초1)부터 17살(고3)까지의 체격(키, 몸무게), 신체조성지수(BMI)값이다. 특히 키, 체중, BMI가 종속변수(반응변수)일 때는 체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율이 예측변수(설명변수, 독립변수)로 하였다<Table 1>. 종속변수의 자료 수집은 교육인적자원부 통계연보에서 체격변인에 해당하는 년 평균자료를 수집하였다. 예측변수(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)의 자료 수집은 통계청 홈페이지의 인구통계와 국가교육과정정보센타(NCIC)에서 수집하였고 예측변수인 체육시설과 체육시간은 종속변수와 초, 중, 고 동일대상이나 동물성식품, GDP디플레이터, 동물성식품섭취분율은 자료 특성상 나이 구분 없이 전 국민을 대상으로 한 자료이므로 종속변수에 맞게 투입 할 수 없는 연구의 한계가 있다는 것을 제한점으로 둔다.
Table 1.
The definition of variables
| Model | Predictor | Response variable | Forecast Period |
|---|---|---|---|
| ARIMA (p,d,q) |
Sports facility(m2) PE (Lessons per week) Animal food(g) GDP deflector(%) Animal food uptake rate(%) |
Height(cm), Weight(kg), BMI(kg/m2) |
long-term (over10years) |
자료처리 방법
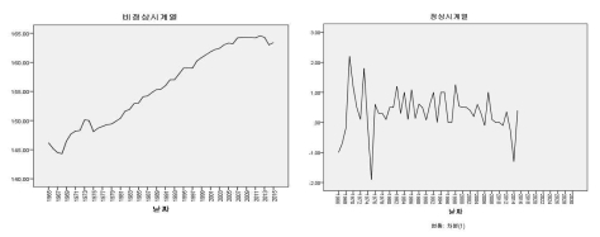
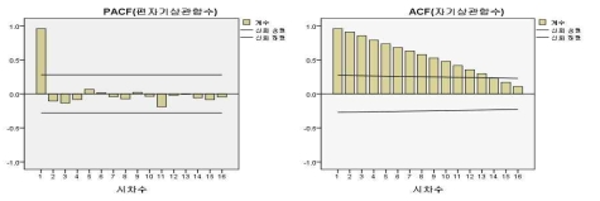
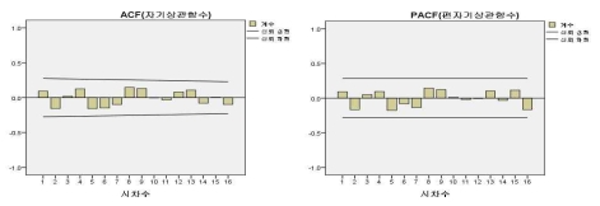
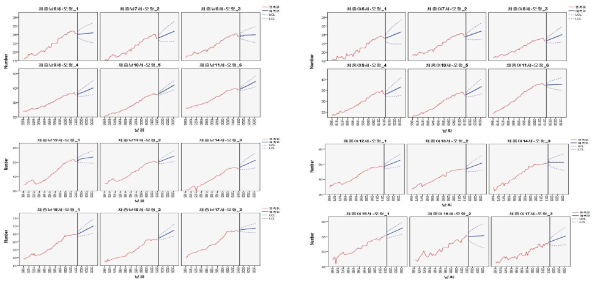
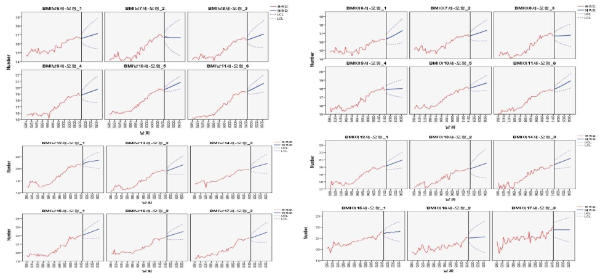
연구목적에 따른 통계처리 방법은 SPSS 22.0을 사용하여 분석하였고 자료의 연산은 Microsoft office Excel 2007을 사용하였다. 시계열 분석을 실시함에 있어 첫째는 추이그래프를 그렸다. 각각의 나이별 신장, 체중, BMI값을 투입하여 정상시계열인지, 비정성시계열인지, 계절성이 있는지 없는지 확인 하였다. 예를 들어 13세 남학생 키의 추세가 있고 분산의 안정화가 필요 할 때는 변환에서 차분(差分, Difference)을 취하여 각각 또는 동시에 그려보면 정상시계열로 변환됨을 알 수 있다<Fig. 1>. 두 번째는 자기상관 플롯·편 자기상관 플롯을 살펴본다. 자기상관이 존재하는지 확인한 결과, 자기상관함수(ACF)의 편자기상관함수(PACF)의 상관계수가 신뢰한계를 넘고 있다<Fig. 2>. 이 자기상관 플롯과 편자기상관 플롯을 보고 ARIMA(p,d,q)모형의 p와 q의 값을 결정한다. 이렇게 결정한 후 차분을 시도한 후 다시 자기상관 플롯과 편자기상관 플롯을 보면 <Fig. 3>과 같이 신뢰구간 안에 상관계수가 존재함을 알 수 있다. 이 때 신뢰한계를 넘는다는 의미는 가설인 m차의 모자기상관계수가 0이라는 영가설을 기각하게 되어 이 시계열자료는 자기상관이 존재한다는 의미이므로 차분을 통해 자기상관이 통계적으로 0을 만족하도록 한다.
세 번째는 최적의 시계열 예측모형을 선택하기위해 Ljung-Box통계량 등으로 모형이 옳은지 체크한다. 즉, SPSS통계프로그램의 시계열분석방법 중 입력계열을 함께 모형 화하여 분석하는 다중시계열 분석방법[다변량ARIMA(p,d,q)]를 선택한다. 예측변인이 있는 ARIMA모형에서 여러 가지 적합도 측도 중 제곱근평균제곱오차(RMSE)를 고려한 최적의 모형을 선택하도록 한다. 입력계열이 있는 ARIMA모형은 다음 3단계인 모형의 식별, 추정, 그리고 진단을 한 주기로 하여 시계열자료에 가장 적합한 모형을 찾는 것이다. 이런 3단계 절차를 박스-젠킨스 법(Box-Jenkins method)이라한다<Table 2>.
Table 2.
ARIMA(p, d, q)Model Creation process
| 1Step | ARIMA(p, d, q) Model Identification |
(1) d difference between the difference |
| (2) Report the ACF and PACF determine the values of p and q | ||
| 2Step | ARIMA(p, d, q) Model Estimationl |
The maximum likelihood estimates of parameters |
| 3Step | ARIMA(p, d, q) Model Diagnosis |
Ljung-Box test for Residuals |
첫 번째인 식별은 계절변동이 아닌 경우 ARIMA(p, d, q)의 p, d, q의 값을 결정 하는 것으로 p는 자기회귀(AR: Autoregressive)부분의 차수를 말하며, d는 difference의 약자로 자료가 추세를 나타낼 경우 차분(계차)을 취하여 정상시계열로 변환하는 것을 말하고, I는 integrated의 약자이다. q는 이동평균(MA: Moving Average)부분의 차수를 정하는 것이다(Table 2). 두 번째, 추정은 AR계수들과 MA계수들의 최우 추정량을 구하는 것이며, 세 번째, 진단은 식별과 추정에 의해 선택된 모형의 적합도를 결정하는 것으로 예측변인인 체육시설(운동장:m2), 체육시간(주당시수),동물성식품(하루육류소비량:g), GDP디플레이터(국가의 총체적인 물가변동지수:(명목 GDP/실질 GDP)×100%), 동물성식품섭취분율(전체식품에서동물성식품이 차지하는 비율:%)을 투입하여 종속변인인 키, 몸무게, BMI의 미래값을 예측하는 분석방법이다(Box & Jenkins, 1975; Dagum, 1975; AKaike, 1978, 1979; Choi, 1992).
연구절차에 따라 산출한 최적의 예측모형의 적절성 여부는 연구모형의 타당성과 신뢰성을 의미한다고 할 수 있으므로 시계열분석 시 적용되는 조건을 다음 3 가지 기준에 따라 모형에 적용하였다. 첫째는 자료의 적절성과 정상성(stationary)이였다. 사용된 체격(신장, 몸무게)자료는 매년 측정, 기록한 등간격인 이산 형으로 측정된 시계열자료이며 자료에 추세가 있어 비정상성을 내포하고 있었으나 차분(d)을 통해 계열의 평균과 분산을 일정하게 유지시키면 모형내의 모수에 대한 유용한 추정값을 얻을 수 있게 된다. 두 번째는 잔차 분석을 통해서 모형을 진단하게 된다(Ljung-Box Q:자기상관계수의 검정). 즉, 정상 시계열모형의 기본 가정은 오차항 et가 백색잡음(백열발광체로부터의 백색광의 연속에너지로부터 유추해서, 광역 진동역에 포함되는 각 진동구간에서 일정한 파워를 갖는 공분산 정상 확률과정:white noise)이며, 오차들은 서로 독립이고, 오차들의 평균은 0이며 분산은 σ2인 정규분포를 따른다는 것이다(Cryer, 1986; Box & Jenkins, 1976; Ljung & Box, 1978; Kim, 2005; Heo, 2010; Noo, 2011).
세 번째는 모형의 선택으로 추정단계에서 자료를 충분히 잘 적합 시키는 모형을 적합도 측도인 제곱근 평균제곱오차(RMSE)를 고려하여 최적의 예측모형이 선정 되었다.
결 과
체격(키, 몸무게), 신체조성지수(BMI)의 합리적인 예측모형을 선정하기 위해 ARIMA(단일/다중)모형을 사용하여 RMSE 적합도를 고려한 최적의 적합도 값을 나타낸 모형을 최종 예측모형으로 선정하였다.
키의 장기예측
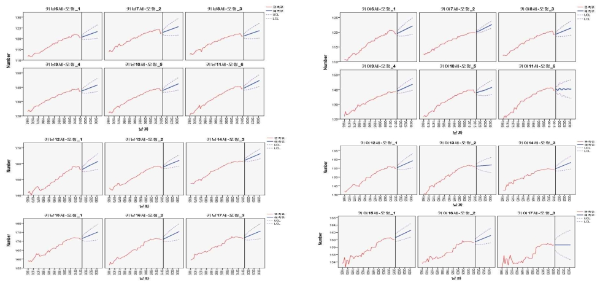
아동·청소년의 키를 예측함에 있어 ARIMA(단일/다중)모형을 이용하여 성별, 나이별로 10년 이상 장기예측 하였다. <Table 3>을 살펴보면 먼저 시계열분석의 가정 중 하나인 잔차의 자기상관이 존재하지 않아야 한다. Ljung-Box Q의 검증을 실시한 결과 모든 모형에서 유의확률 p는 유의수준 .05보다 크므로, 잔차의 자기상관이 존재하지 않아야하는 가정에 위반 되지 않았다. 또한 투입된 예측자수를 살펴보면 총 5개(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)중 유의미한(p<0) 예측변수만 투입된다. 남자인 경우는 12세의 ARIMA (0, 1, 0)모형에서 2개(체육시설, 체육시간)의 유의미한 예측변수가 적용되었고 13세의 ARIMA(0, 1, 0)모형에서는 체육시간, 1개가 적용되었다. 여자인 경우는 7세의 ARIMA(0, 1, 1)모형에서 동물성식품이, 10세의 ARIMA(0, 1, 0)모형에서 체육시설이, 11세의 ARIMA (0, 1, 0)모형에서 동물성식품이, 12세의 ARIMA(0, 1, 0)모형에서 체육시간이, 13세의 ARIMA(0, 1, 0)모형에서 동물성식품이, 각각 1개씩 예측변수로 적용되었다. <Fig. 4>의 남·여 예측선을 살펴보면 남자나 여자 모두 증가추세이나 여자 중 11세는 감소하다 증가하는 추세였다.
Table 3.
n=51
| gender | grade | years | Model Type | Number of Predictor | Goodness of fit | Ljung-BoxQ(18) | Predictive values(cm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | statistic | df | p | 2020 | 2025 | 2030 | |||||
| Male | E1 | 6Y | ARIMA(0,1,0) | 0 | .39 | 7.37 | 18 | .987 | 121.38 | 122.26 | 123.14 |
| E2 | 7Y | ARIMA(0,1,0) | 0 | .61 | 11.70 | 18 | .862 | 127.02 | 128.14 | 129.26 | |
| E3 | 8Y | ARIMA(0,1,0) | 0 | .65 | 15.74 | 18 | .611 | 132.85 | 134.10 | 135.35 | |
| E4 | 9Y | ARIMA(0,1,0) | 0 | .57 | 9.20 | 18 | .955 | 138.51 | 139.92 | 141.33 | |
| E5 | 10Y | ARIMA(0,1,0) | 0 | .54 | 13.45 | 18 | .764 | 144.05 | 145.60 | 147.15 | |
| E6 | 11Y | ARIMA(1,1,0) | 0 | .68 | 8.25 | 17 | .961 | 150.79 | 152.62 | 154.44 | |
| M1 | 12Y | ARIMA(0,1,0) | 2 | .61 | 18.53 | 18 | .421 | 157.77 | 159.49 | 161.12 | |
| M2 | 13Y | ARIMA(0,1,0) | 1 | .58 | 7.23 | 18 | .988 | 165.41 | 167.29 | 169.08 | |
| M3 | 14Y | ARIMA(0,1,0) | 0 | .54 | 14.97 | 18 | .664 | 171.00 | 172.90 | 174.80 | |
| H1 | 15Y | ARIMA(0,1,0) | 0 | .55 | 12.97 | 18 | .793 | 172.52 | 173.74 | 174.96 | |
| H2 | 16Y | ARIMA(0,1,0) | 0 | .44 | 20.90 | 18 | .285 | 173.84 | 174.98 | 176.12 | |
| H3 | 17Y | ARIMA(0,1,0) | 0 | .42 | 14.22 | 18 | .715 | 174.38 | 175.36 | 176.34 | |
| Female | E1 | 6Y | ARIMA(0,1,0) | 0 | .35 | 10.99 | 18 | .895 | 120.26 | 121.12 | 121.98 |
| E2 | 7Y | ARIMA(0,1,1) | 1 | .38 | 11.44 | 17 | .833 | 127.85 | 129.29 | 130.77 | |
| E3 | 8Y | ARIMA(0,1,0) | 0 | .50 | 11.65 | 18 | .865 | 131.49 | 132.68 | 133.87 | |
| E4 | 9Y | ARIMA(1,1,0) | 0 | .76 | 27.59 | 17 | .050 | 140.19 | 141.76 | 143.35 | |
| E5 | 10Y | ARIMA(0,1,0) | 1 | .61 | 18.50 | 18 | .423 | 143.95 | 144.90 | 146.29 | |
| E6 | 11Y | ARIMA(0,1,0) | 1 | .79 | 15.36 | 18 | .637 | 150.95 | 150.21 | 150.27 | |
| M1 | 12Y | ARIMA(0,1,0) | 1 | .50 | 15.12 | 18 | .654 | 156.41 | 157.72 | 159.03 | |
| M2 | 13Y | ARIMA(0,1,0) | 1 | .44 | 13.05 | 18 | .788 | 158.10 | 158.25 | 158.45 | |
| M3 | 14Y | ARIMA(1,1,0) | 0 | .61 | 16.78 | 17 | .469 | 160.68 | 161.87 | 163.07 | |
| H1 | 15Y | ARIMA(0,1,1) | 0 | .55 | 9.11 | 17 | .937 | 161.13 | 161.80 | 162.48 | |
| H2 | 16Y | ARIMA(0,1,1) | 0 | .35 | 10.23 | 17 | .894 | 161.12 | 161.67 | 162.22 | |
| H3 | 17Y | ARIMA(1,0,0) | 5 | .56 | 17.68 | 17 | .409 | 161.37 | 161.42 | 161.43 | |
몸무게의 장기예측
몸무게를 예측함에 있어 ARIMA(단일/다중)모형을 이용하여 성별, 나이별로 10년 이상 장기예측 하였다<Table 4>. 먼저 Ljung-Box Q의 검증을 실시한 결과 잔차의 자기상관이 존재하지 않았다(p>.05). 또한 투입된 예측자수는 5개(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)로 몸무게를 예측함에 있어 남자의 경우, 6세는 ARIMA(0, 1, 0)모형에서 체육시간이, 8세는 ARIMA(0,1,0)모형에서 동물성식품이, 12세 ARIMA(0,1,0)에서 GDP디플레이터가, 13세는 ARIMA(0,1,0)모형에서 체육시간이, 14세는 ARIMA(0,1,0)모형에서 체육시설이, 15세는 ARIMA (0,1,0)에서 동물성식품섭취분율이, 각각 1개씩 유의미한 예측변인으로 사용되었으며, 17세는 ARIMA(0,1,0)에서 2개의 예측변인인 GDP디플레이터와 체육시간이 적용 되었다. 또한 5개의 예측변인이 적용된 경우는 11세의 ARIMA(0,1,1)모형에서 나타났다. 여학생의 몸무게를 예측한 경우, 11세는 ARIMA(0,1,0)에서 GDP 디플레이터가, 14세는 ARIMA(0,1,0)에서 동물성식품이, 16세는 ARIMA(0,1,0)에서 동물성식품이 각각 1개씩 사용되었고 2개(체육시설, 체육시간)의 예측변인이 사용된 경우는 9세의 ARIMA(0,1,0)모형만 이였다. 또한 예측값을 살펴보면 남자나 여자 모두 2030년까지 증가추세가 될 것으로 예측 하였다<Fig. 5>.
Table 4.
n=51
| gender | grade | years | Model Type | Number of Predictor | Goodness of fit | Ljung-BoxQ(18) | Predictive values(kg) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | statistic | df | p | 2020 | 2025 | 2030 | |||||
| Male | E1 | 6Y | ARIMA(0,1,0) | 1 | .29 | 11.83 | 18 | .856 | 24.15 | 24.27 | 24.40 |
| E2 | 7Y | ARIMA(0,1,0) | 0 | .40 | 10.58 | 18 | .911 | 27.92 | 28.64 | 29.36 | |
| E3 | 8Y | ARIMA(0,1,0) | 1 | .46 | 18.42 | 18 | .428 | 31.74 | 31.82 | 31.93 | |
| E4 | 9Y | ARIMA(0,1,0) | 0 | .47 | 9.50 | 18 | .947 | 36.74 | 38.24 | 39.80 | |
| E5 | 10Y | ARIMA(1,1,0) | 0 | .41 | 12.73 | 17 | .754 | 42.62 | 44.66 | 46.80 | |
| E6 | 11Y | ARIMA(0,1,1) | 5 | .45 | 27.15 | 17 | .057 | 45.32 | 45.63 | 46.05 | |
| M1 | 12Y | ARIMA(0,1,0) | 1 | .54 | 19.76 | 18 | .347 | 52.41 | 52.99 | 53.54 | |
| M2 | 13Y | ARIMA(0,1,0) | 1 | .62 | 12.67 | 18 | .811 | 58.36 | 60.29 | 62.14 | |
| M3 | 14Y | ARIMA(0,1,0) | 1 | .87 | 10.01 | 18 | .932 | 63.72 | 65.88 | 68.04 | |
| H1 | 15Y | ARIMA(0,1,0) | 1 | .55 | 17.29 | 18 | .504 | 66.23 | 67.97 | 69.73 | |
| H2 | 16Y | ARIMA(0,1,1) | 0 | .52 | 13.15 | 17 | .726 | 68.67 | 70.39 | 72.14 | |
| H3 | 17Y | ARIMA(0,1,0) | 2 | .30 | 23.64 | 18 | .167 | 69.12 | 69.40 | 69.68 | |
| Female | E1 | 6Y | ARIMA(0,1,0) | 0 | .34 | 20.78 | 18 | .291 | 23.59 | 24.08 | 24.57 |
| E2 | 7Y | ARIMA(0,1,0) | 0 | .32 | 10.23 | 18 | .924 | 26.30 | 26.90 | 27.50 | |
| E3 | 8Y | ARIMA(0,1,0) | 0 | .37 | 18.73 | 18 | .409 | 30.01 | 30.95 | 31.91 | |
| E4 | 9Y | ARIMA(0,1,0) | 2 | .42 | 12.65 | 18 | .812 | 34.03 | 35.18 | 36.36 | |
| E5 | 10Y | ARIMA(0,1,0) | 0 | .47 | 27.66 | 18 | .067 | 39.35 | 40.97 | 42.65 | |
| E6 | 11Y | ARIMA(0,1,0) | 1 | .39 | 14.11 | 18 | .722 | 43.74 | 43.87 | 44.00 | |
| M1 | 12Y | ARIMA(0,1,0) | 0 | .50 | 18.03 | 18 | .454 | 49.58 | 50.96 | 52.34 | |
| M2 | 13Y | ARIMA(0,1,0) | 0 | .61 | 8.69 | 18 | .966 | 52.92 | 54.24 | 55.56 | |
| M3 | 14Y | ARIMA(0,1,0) | 1 | .45 | 13.30 | 18 | .774 | 54.21 | 54.07 | 54.25 | |
| H1 | 15Y | ARIMA(0,1,1) | 0 | .52 | 6.93 | 17 | .985 | 56.20 | 57.00 | 57.80 | |
| H2 | 16Y | ARIMA(0,1,0) | 1 | .41 | 11.31 | 18 | .881 | 56.11 | 56.18 | 56.26 | |
| H3 | 17Y | ARIMA(1,1,0) | 0 | .41 | 15.38 | 17 | .568 | 57.05 | 57.58 | 58.12 | |
BMI의 장기예측
신체질량지수(BMI)를 예측함에 있어 ARIMA(단일/다중)모형을 이용하여 성별, 나이별로 10년 이상 장기예측 하였다. <Table 5>을 살펴보면 제일 먼저 잔차의 자기상관이 존재하지 않아야 하는 가정이 만족하는지 Ljung-Box Q의 검증을 실시한 결과 모든 모형에서 유의확률값이 유의수준 .05보다 크므로, 잔차의 자기상관이 존재하지 않아야하는 가정에 위반 되지 않았다. 또한 적합도인 제곱근평균제곱오차(RMSE)를 고려한 최적의 모형을 자동으로 선택하도록 하였다.
Table 5.
n=51
| gender | grade | years | Model Type | Number of Predictor | Goodness of fit | Ljung-BoxQ(18) | Predictive values(kg/m2) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | statistic | df | p | 2020 | 2025 | 2030 | |||||
| Male | E1 | 6Y | ARIMA(1,0,1) | 5 | .20 | 21.46 | 16 | .161 | 16.82 | 16.85 | 16.89 |
| E2 | 7Y | ARIMA(0,1,0) | 1 | .21 | 21.06 | 18 | .276 | 17.15 | 17.15 | 17.15 | |
| E3 | 8Y | ARIMA(0,1,0) | 0 | .23 | 23.67 | 18 | .166 | 18.13 | 18.39 | 18.65 | |
| E4 | 9Y | ARIMA(0,1,0) | 0 | .26 | 19.22 | 18 | .378 | 19.07 | 19.38 | 19.68 | |
| E5 | 10Y | ARIMA(1,1,0) | 0 | .18 | 19.12 | 17 | .321 | 20.00 | 20.38 | 20.76 | |
| E6 | 11Y | ARIMA(0,1,0) | 1 | .16 | 15.51 | 18 | .627 | 20.71 | 21.14 | 21.57 | |
| M1 | 12Y | ARIMA(0,1,1) | 5 | .20 | 22.81 | 17 | .155 | 20.63 | 20.42 | 19.97 | |
| M2 | 13Y | ARIMA(0,1,0) | 0 | .21 | 17.03 | 18 | .521 | 21.48 | 21.86 | 22.25 | |
| M3 | 14Y | ARIMA(0,1,0) | 1 | .29 | 12.31 | 18 | .831 | 22.17 | 22.53 | 22.89 | |
| H1 | 15Y | ARIMA(1,1,0) | 0 | .17 | 22.73 | 17 | .158 | 22.25 | 22.49 | 22.73 | |
| H2 | 16Y | ARIMA(1,1,0) | 0 | .18 | 6.63 | 17 | .988 | 22.66 | 22.90 | 23.13 | |
| H3 | 17Y | ARIMA(0,1,0) | 0 | .15 | 21.06 | 18 | .276 | 22.91 | 23.14 | 23.37 | |
| Female | E1 | 6Y | ARIMA(0,1,0) | 5 | .28 | 16.85 | 18 | .534 | 16.43 | 16.69 | 17.01 |
| E2 | 7Y | ARIMA(0,1,0) | 0 | .23 | 18.30 | 18 | .436 | 16.74 | 16.89 | 17.04 | |
| E3 | 8Y | ARIMA(0,1,0) | 1 | .16 | 24.01 | 18 | .155 | 17.12 | 17.19 | 17.26 | |
| E4 | 9Y | ARIMA(0,1,1) | 5 | .23 | 19.33 | 17 | .310 | 17.94 | 17.97 | 17.97 | |
| E5 | 10Y | ARIMA(0,1,0) | 5 | .17 | 18.89 | 18 | .399 | 18.85 | 19.14 | 19.44 | |
| E6 | 11Y | ARIMA(0,1,0) | 2 | .15 | 18.09 | 18 | .450 | 19.55 | 19.61 | 19.65 | |
| M1 | 12Y | ARIMA(0,1,1) | 0 | .22 | 17.73 | 17 | .406 | 20.37 | 20.65 | 20.92 | |
| M2 | 13Y | ARIMA(0,1,0) | 0 | .25 | 16.25 | 18 | .575 | 20.98 | 21.23 | 21.48 | |
| M3 | 14Y | ARIMA(0,1,1) | 0 | .20 | 13.43 | 17 | .707 | 21.38 | 21.57 | 21.75 | |
| H1 | 15Y | ARIMA(0,1,0) | 2 | .11 | 12.54 | 18 | .818 | 21.50 | 21.53 | 21.60 | |
| H2 | 16Y | ARIMA(0,1,0) | 1 | .16 | 18.80 | 18 | .404 | 21.78 | 21.82 | 21.86 | |
| H3 | 17Y | ARIMA(0,1,1) | 0 | .20 | 9.02 | 17 | .940 | 21.73 | 21.73 | 21.73 | |
그 결과 투입된 5개의 예측자수(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)중 유의미한(p<0.5) 예측변수만 선택되어 남자인 경우는 6세에서 ARIMA(1,0,1)모형, 12세에서 ARIMA(0,1,1) 모형 이 5개 예측변수 모두 적용되었고 7세는 ARIMA(0,1,0)모형에서 체육시설이, 11세는ARIMA(0,1,0)모형에서 체육시간이, 14세는 ARIMA(0,1,0)모형에서 체육시설이 각각 1개씩 예측변수로 적용되었다. 여자인 경우는 6세ARIMA(0,1,0)모형, 9세ARIMA(0,1,1)모형, 10세 ARIMA(0,1,0)모형에서는 5개의 예측자수가 모두 적용되었고 11세ARIMA(0,1,0)모형에서는 동물성식품과 체육시간이, 15세 ARIMA(0,1,0)모형에서는 동물성식품과 체육시설이 각각 2개씩의 예측변수가 적용되었다.
또한 8세의 ARIMA(0,1,0)모형에서는 체육시간이 16세의 ARIMA(0,1,0)모형에서는 동물성식품이 각각 1개씩의 예측변수만 적용되었다. 이러한 결과로 <Fig. 6>의 예측함수곡선을 살펴보면 2030년까지 남자나 여자 모두 증가추세이나 여자 중 9세와 17세에서는 거의 정체를 나타내고 있을 것으로 예측하였다.
논의 및 결론
본 연구의 목적을 달성하기위해 1965년부터 2015년까지의 연간평균자료인 키, 몸무게, BMI자료를 이용, 입역계열(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)이 있는 자기회귀통합이동평균[ARIMA(p,d,q)]모형을 적용하여 키, 몸무게, BMI의 예측모형과 예측값을 나이 별로 제시한다.
첫째, 아동·청소년의 신장 예측함에 있어 남학생의 예측모형은 11세인 경우에만 ARIMA(0,1,0)모형이였고 나머지 모형은 ARIMA(0,1,0)모형 이였다. 또한 2030년의 예측값을 나이별로 제시하면, 6세(초1)는 123.14cm, 7세(초2)는 129.26cm, 8세(초3)은 135.35cm, 9세(초4)는 141.33cm, 10세(초5)는 147.15cm, 11세(초6)는 154.44cm, 12세(중1)는 161.12cm, 13세(중2)는 169.08cm, 14세(중3)는 174.80cm, 15세(고1)는 174.96cm, 16세(고2)는 176.12cm, 17세(고3)는 176.34cm이였다. 여자인 경우는 ARIMA(0,1,0) 모형이 6세, 8세, 10세, 11세, 12세, 13세 이였고 ARIMA(0,1,1)모형은 7세, 15세, 16세 이였으며, ARIMA(1,1,0)모형은 9세, 14세, ARIMA(1,0,0)모형은 17세 하나였다. 또한 2030년의 예측값을 나이별로 제시하면, 6세(초1)는 121.98cm, 7세(초2)는 130.77cm, 8세(초3)은 133.87cm, 9세(초4)는 143.35cm, 10세(초5)는 146.29cm, 11세(초6)는 150.27cm, 12세(중1)는 159.03cm, 13세(중2)는 158.45cm, 14세(중3)는 163.07cm, 15세(고1)는 162.48cm, 16세(고2)는 162.22cm, 17세(고3)는 161.43cm이였다.
전체적인 예측 키 추세 특징은 남·여 모두 증가추세이나 여학생의 11세, 13세, 17세에서 증가율이 낮게 나타나고 있었다.
둘째, 체중을 예측함에 있어 남학생의 예측모형은 ARIMA(0,1,0)모형이 대부분 이였고 6, 7, 8, 9세와 12, 13, 14, 15, 17세가 이 경우에 해당되었다. ARIMA(0,1,1)모형은 11세와 16세 이였고, ARIMA(1,1,0)모형은 10세뿐 이였다. 또한 2030년의 예측값을 나이별로 제시하면, 6세(초1)는 24.4kg, 7세(초2)는 29.36kg, 8세(초3)은 31.93kg, 9세(초4)는 39.8kg, 10세(초5)는 46.8kg, 11세(초6)는 46.05kg, 12세(중1)는 53.54kg, 13세(중2)는 62.13kg, 14세(중3)는 68.04kg, 15세(고1)는 69.73kg, 16세(고2)는 72.14kg, 17세(고3)는 69.68kg이였다.
여학생의 체중인 경우도 ARIMA(0,1,0)모형이 대부분 이였고 6세 - 14세와 16세가 이 모형에 해당되었다. 또한 ARIMA(1,1,0)모형은 17세뿐 이였고 ARIMA(0,1,1)모형도 15세뿐 이였다. 또한 2030년의 예측값을 나이별로 제시하면, 6세(초1)는 24.57kg, 7세(초2)는 27.5kg, 8세(초3)은 31.91kg, 9세(초4)는 36.36kg, 10세(초5)는 42.65kg, 11세(초6)는 44kg, 12세(중1)는 52.34kg, 13세(중2)는 55.56kg, 14세(중3)는 54.25kg, 15세(고1)는 57.8kg, 16세(고2)는 56.26kg, 17세(고3)는 58.12kg이였다. 전체적인 체중의 예측추세 특징은 남·여 모두 증가추세인 것으로 나타나고 있으며, 키의 증가율에 비해 높게 나타나고 있었다.
셋째, BMI를 예측함에 있어 남학생의 ARIMA(0,1,0)모형은 7, 8, 9, 11, 13, 14, 17세가 이 경우에 해당되었다. ARIMA(1,1,0)모형은 10세와 15, 16세 이였고, ARIMA(0,1,1)모형은 12세뿐 이였다.
또한 2030년의 남학생의 BMI 예측값을 나이별로 제시하면, 6세(초1)는 16.89, 7세(초2)는 17.15, 8세(초3)은 18.65, 9세(초4)는 19.68, 10세(초5)는 20.76, 11세(초6)는 21.57, 12세(중1)는 19.97, 13세(중2)는 22.25, 14세(중3)는 22.89, 15세(고1)는 22.73, 16세(고2)는 23.13, 17세(고3)는 23.37이였다.
여학생인 경우의 BMI 예측모형은 ARIMA(0,1,0)모형이 대부분 이였고 이 모형은 6세, 7세, 8세, 10세, 11세, 13세, 15세,16세에서 적용되었다. 나머지 9세, 12세, 14세, 17세는 ARIMA(0,1,1)모형이 적용되었다. 또한 여학생의 2030년 BMI예측값을 나이별로 제시하면, 6세(초1)는 17.01, 7세(초2)는 17.04, 8세(초3)은 17.26, 9세(초4)는 17.97, 10세(초5)는 19.44, 11세(초6)는 19.65, 12세(중1)는 20.92, 13세(중2)는 21.48, 14세(중3)는 21.75, 15세(고1)는 21.6, 16세(고2)는 21.86, 17세(고3)는 21.73 이였다. 전체적인 BMI의 예측추세 특징은 남·여 모두 증가추세로 나타나고 있으며 증가추세가 키에 비해서는 크고 몸무게에 비해서는 비슷한 추세를 보이고 있었다. 특히 초6, 중2, 중3, 고2, 고3 남학생의 평균 BMI가 22-23이였다.
최근 아동·청소년들의 놀이문화는 집 컴퓨터게임 아니면 핸드폰 게임, 게임기 오락, PC방에서 게임, TV시청등 신체활동과 거리가 먼 놀이문화로 이들 게임으로 하루시간을 대부분 차지하고 있다. 2003년도에 한국 청소년 개발원에서 조사한 바에 따르면, 전체 청소년 응답자의 69.8%가 인터넷을 거의 매일 사용하고 있는 것으로 드러났다. 이들이 인터넷을 이용하는 목적으로는 여러 가지가 있지만 이 중 게임과 오락이 28.7%로 가장 높은 수치를 보이고 있다(Lee, 2003). 이러한 결과는 아동·청소년의 비만의 원인이 되고 있다. 청소년의 비만은 성인비만과 상관이 높다는 연구결과도 있으며(Kim & Kim, 2013), 국가의료비지출의 부담이 커져만 가고 있다. 따라서 아동·청소년의 키, 몸무게, BMI의 예측은 비만 유병률의 증가 속에서 학생들과 학부모를 비롯한 국가에게 미래에 대한 건강의 중요성을 인식시키고 국가 정책을 수립하는데 판단기준이 되도록 하기 위함이며, 또한 이들 청소년들이 성장하여 국가의 중추기관을 맡을 인재인 만큼 이들의 체격과 신체조성이 어떻게 변화해 갈 것인가를 예측한다는 것은 더욱 중요하리라 예상된다.
이러한 중요성으로 비춰볼 때 지금까지 시계열분석을 이용한 기존의 스포츠관련 논문은 주로 단변량ARIMA(p,d,q)모형 이였지만 본 논문은 입역계열(체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율)이 있는 다변량 자기회귀통합이동평균인 ARIMA(p,d,q)모형을 사용한 점이 기존의 논문과 다르다. 또한 본 논문의 연구결과와 유사한 논문은 아직 찾지 못하였으나 비록 예측값을 제시하지는 못하였으나 아동·청소년의 체격·체력의 추세가 증가하는지 감소하는지를 살펴본 Chae & Shin(2015)의 논문이 본 연구와 맥을 같이한다. 또한 모형선택방법에 있어 Kim & Chae(2012)은 최적의 모형 4개 중 추세회귀모형과 단변량 최근린법은 BIC 통계량이 산출 되지 않으므로 BIC기준이 적용되지 않았고 나머지 2개 모형인 자동 생성모형과 다변량ARIMA모형에서만 적용 하였다고 하였다. 이에 비해 본 논문은 최적의 시계열 예측모형을 선택하기위해 시계열분석방법 중 입력계열을 함께 모형화하여 분석하는 다중시계열 분석 방법을 선택하여, 예측변인이 있는 ARIMA모형에서 Ljung-Box Q의 검증을 거친 후 통과한 모형 중에서 여러 가지 적합도 측도 중 제곱근평균제곱오차(RMSE)가 가장 적은 모형으로 선택하도록 하였다.
이상 본 연구결과를 통해 예측변수인 학교체육시설인 운동장 감소, 체육시간 축소, 동물성식품섭취 증가 등이 비만의 원인이 될 수 있으며, 본 연구에서 예측변인으로 제시하지 못 했지만 신체활동과 거리가 먼 놀이문화(컴퓨터게임, 핸드폰 게임, 오락기기게임)의 증가 또한 그 원인이라 여겨진다. 시계열자료의 특징은 시차가 있는 자료를 분석하는 것으로 특성은 같고 시차만 있는 것이다. 즉, 시간에 흐름에 따라 관측된 자료로써, 가까운 관측시점의 자료일수록 관측된 자료들 간에 상관관계가 크다. 보통 연도별, 분기별, 월별, 주별 데이터를 사용하는데 원자료 대신 계절대비증감률, 전년도대비 증감률, 기준지수100, 평균지수 등을 사용하기도 한다. 본 자료는 연도별 평균자료를 사용하고 있다. 본 연구의 예측변인인 체육시설, 체육시간, 동물성식품, GDP디플레이터, 동물성식품섭취분율 외 컴퓨터게임 또는 핸드폰게임시간, 탄산음료섭취량, 방과 후 학원 또는 과외지속시간을 또 다른 예측변수로 생각 할 수 있겠다. 또한 본 연구의 예측변수인 체육시설과 체육시간은 종속변수와 초, 중, 고 동일대상으로 적용되었으나 동물성식품, GDP디플레이터, 동물성식품섭취분율은 자료 특성상 나이 구분 없이 전 국민을 대상으로 한 자료뿐이므로 종속변수대상에 맞게 투입 할 수 없는 연구의 한계가 있었다는 것을 말씀드리며, 현재 각 연령층에서 나타나고 있는 BMI의 증가 추세는 외국의 사례를 보아도 알 수 있듯이 비만은 국민건강을 위협하며, 의료비가 증가하는 국가적 사태로 발전되고 있는 상황을 정부는 예의 주의 할 것이며, 정부에서 실시하고 있는 국민체력 100사업과 연계하여 아동·청소년의 신체활동을 더욱 강력하게 늘리는 계획을 실천해야한다.
2013년 한국연구재단의 지원을 받아 수행된 연구. (NRF-2013S1A5B5A01027910)
References
2013 National Health Statistics: National Health and Nutrition Examination Survey (Centers for Disease Control and Prevention) (2013) Centers for Disease Control and Prevention. (2013). 2013 National Health Statistics: National Health and Nutrition Examination Survey, 6th primary year. , 6th primary year
KATS - Konkuk University sign MOU for human standard information literacy and digital technology Fashion Clothing (Korean Agency for Technology and Standards) (2007) korea: KDI Korean Agency for Technology and Standards(2007). KATS - Konkuk University sign MOU for human standard information literacy and digital technology Fashion Clothing, korea: KDI.
, Stefani, R.T. (2003) ‘‘Estimating the Probability of a Home Win, Draw and Away Win in Soccer’’, , Proceedings of the International Statistical Institute, , 13-20 August, Berlin, Germany., , 2003, ‘‘Estimating the Probability of a Home Win, Draw and Away Win in Soccer’’, Proceedings of the International Statistical Institute, 13, 20, August, Berlin, Germany