ISSN : 1598-2920
In this paper, effects on the match outcome of the various scoring methods frequently used in doubles tennis matches were analyzed using a simple probabilistic theory. It was assumed that the outcome of a single point depends on the server’s point-winning probability, which was assumed to be an independent event with an identical distribution for each point. It was found that the game-winning probability of the server’s team is greater than 0.5 - at times significantly higher - for server’s point-winning probability larger than 0.5, with the traditional game scoring method yielding the highest probability, followed by ‘one-deuce no-ad’ and then ‘no-ad rules’. For doubles matches between two ‘even-strength’ players on each team, which is essentially the same as singles matches, the order of the set-winning probability for the team with the first service game, as arranged in the order of the highest to the lowest, was: the traditional format (win-by-two-games), deuce games/tiebreak at six-games-all format, no-ad games/tiebreak at six-games-all format, one-deuce-no-ad games/tiebreak at five-games-all format, and finally no-ad games/tiebreak at five-games-all format, for the cases of point-winning probability larger than 0.5. In doubles matches involving teams with uneven average strengths or uneven partner skills, it was determined that the set-winning probability depends critically not only on the composition of the partners and service-game order but also on the scoring methods as well.
본 연구에서는 테니스 복식 경기에서 사용하는 각종 점수 산정 방식에 따른 승률을 간단한 확률 모형을 이용하여 계산하였다. 한 포인트의 향방은 서브권자의 득점 확률에 따른다고 가정하였으며, 이 사건은 독립적이고 동일한 확률 분포를 따른다고 가정하였다. 한 선수의 서브권 득점 확률이 0.5 보다 크면 게임 획득 확률이 0.5보다 급격하게 커지며, 전통적 방식, 1듀스 노애드 방식, 노애드 방식의 순으로 그 값이 크다. 동일한 실력을 지닌 선수로 이루어진 복식 팀 간의 승패는 단식의 결과로 해석할 수 있는데, 서브권 득점 확률이 0.5 보다 큰 경우에 전통적 방식, 듀스-6올 타이브레이크 방식, 노애드-6올 타이브레이크 방식, 1듀스 노애드-5올 타이브레이크 방식, 노애드-5올 타이브레이크 방식의 순으로 세트 획득 확률이 낮아진다. 서브권 득점 확률이 다른 네 명의 선수가 복식 시합을 하게 되면, 세트 획득 확률이 팀의 구성 및 서브의 순서 뿐 만 아니라 점수 산정 방식에도 적지 않은 영향을 받게 된다.
프로 테니스 경기에서 전통적 듀스 게임 방식으로 시합을 진행하면 경기 시간이 지나치게 길어지는 가능성이 있을 수 있다. 이 때문에 선수들의 체력 저하로 인한 부상의 우려가 있고, 관중들이 지루함을 느껴 경기 관람에 대한 흥미가 떨어질 수 있으며, 또한 TV 중계방송 시간이 늘어나는 등의 폐단이 있을 수 있다. 이를 개선하기 위하여 국제테니스연맹(ITF: International Tennis Federation)은 여러 차례에 걸쳐 경기 규정을 개정하여 왔다(ITF Rule). 특히 프로 선수들에게 단식뿐만 아니라 복식에도 참여할 기회를 제공하기 위해서 경기 시간을 단축시키는 경기 규정을 2006년도부터 적용하고 있다. 많은 복식의 국제 시합의 점수 산정 방식은 노애드 방식으로 게임의 승부를 결정하고, 게임 스코어가 6:6(게임 듀스)인 경우에는 7-점 타이브레이크 방식을 적용하여 세트를 결정하고, 세트 스코어가 1:1(세트 듀스)이 되면 마지막 세트는 7-점 타이브레이크 또는 10-점 타이브레이크(match tie-break이라고도 함)로 대체하기로 하였다.
국내에서는 약 30만 명의 동호인들이 테니스를 즐기고 있으며, 대부분이 복식을 위주로 경기를 하고 있다고 알려져 있다(이홍구와 한태룡, 2004). 이들은 소속 지역, 직장 등의 클럽에서 여가활동의 일환으로 테니스 경기를 하지만 그 중 약 3만 명은 지역 단위 또는 전국 규모로 개최되는 동호인 랭킹 시합에도 활발히 참여하고 있다(Tennis People Statistics). 동호인의 시합에서는 주로 한 세트로 승부를 결정하는 것이 현실이며, 경기 진행은 전통적 방식 이외에도 다양한 방식을 적용하여 이루어지고 있다. 전국 규모의 동호인의 공식 시합은 주로 한국테니스진흥협회(KATA), 한국테니스발전협의회(KATO), 국민생활체육전국테니스연합회(KTFS)의 3개 단체가 주관하고 있는데, 노애드(no-ad) 방식으로 게임을 진행하고, 타이브레이크(tie-break) 방식으로 한 세트로 승패를 결정짓도록 하는 방식이 채택되고 있다. 한 세트로 승부를 결정함에도 일부 대회의 예선 또는 본선에서도 6 게임 올인 경우 7-점 타이브레이크를 적용하는 것이 아니라 속칭 ‘5 올 타이브레이크’ 방식, 즉 5 올인 경우 바로 7-점 타이브레이크를 적용하는 점수 산정 방식이 채택되고 있다. 그런데 이들 3개 단체는 5 올 타이브레이크 방식에 관한 규정을 명시적으로 밝히지 않고 있으므로 이는 경기 진행 일정상 등의 이유로 만들어진 관습적인 규칙이라고 여겨진다. KTFS만이 자체 경기 규정을 갖고 있지만 5-5 타이브레이크 방식에 관한 규정은 포함되어 있지 않다(KTFS Rule). 또한, 많은 지역 대회에서도 이러한 방식이 사용되고 있는 실정이다.
테니스 경기는 모든 스포츠 종목과 마찬가지로 경기가 객관적으로 판단하였을 때 공정하게 진행되어야 하는 것이 원칙이라 할 수 있다. 여기서는 공정성을 다음과 같은 의미로 파악하였다. 첫째, 경기에 참가한 모든 선수에게 공평한 기회가 제공되어야 함을 의미하고, 둘째, 객관적인 측면에서 실력이 우수한 선수(복식에서는 복식 조)가 승리할 확률이 높은 것을 의미하고, 셋째, 경기 방식의 채택이 승부에 주는 영향이 적어야함을 의미한다. 또한, 국제적으로 공인된 규정에 의거하여 시합이 진행되어야 한다고 여겨진다.
테니스 경기는 서브권에서 한 포인트가 결정되는 확률을 정할 수 있다면 승패의 확률을 쉽게 계산할 수 있다(Barnett, 2013; Barnett & Clarke, 2002; Brody, 2003). 물론 서브권에서의 득점 확률만으로 승패의 예측을 하는 데는 제약이 있을 수 있고 이를 위해 국내외의 선행연구가 있어 왔다(유현조와 황영성, 2012; 이성국, 2006; 최형준과 김주학, 2006; 최형준과 김주학, 2009; Klaassen & Magnus, 2003; Knottenbelt et al., 2012; Spanias & Knottenbelt, 2012). 특히, 이성국이 국내 동호인 복식 경기를 연구한 결과 및 유현조와 황영성이 2011년 호주 오픈 남자 복식 경기를 연구한 결과에 따르면 서브권에서의 득점 확률이 경기 승패에 중요한 변인임을 알 수 있다.
복식 경기는 확률론적 관점에서 불공정성이 내재되어 있다고 알려져 있다. 이는 첫째로 복식에 참여하는 선수가 팀당 2명씩이므로 총 4명인 점과 서브권을 가진 선수가 유리할 수 있다는 점에서 기인한다. 모든 선수에게 동등한 기회를 제공하기 위해서는 4의 배수가 되도록 게임 수를 진행하여야 하지만 한 팀이 6 게임을 2 게임 차이 이상으로 선취하면 한 세트가 끝나게 된다. 이 때, 모든 선수에게 동일하게 서브권을 행사할 기회가 주어지지 않은 경우가 발생할 수 있기 때문이다(Pollard, 2005; Pollard et al., 2007). 또 다른 불공정성은 게임 듀스 즉(6:6)에서 7-점 타이브레이크 방식으로 그 세트의 승패가 결정됨에 기인한다. 타이브레이크가 진행되면 첫 선수는 한 번의 서브권을 갖지만 그 후에는 각 선수가 두 번의 서브권을 가지므로 승패의 확률이 전통적인 듀스 게임과는 다르게 나타나게 된다(Pollard & Noble, 2003a & 2003b). 또한 5-5에서 타이브레이크를 진행하면 승패의 확률이 다르게 나타난다.
이러한 다양한 선행 연구에도 불구하고, 현재까지는 앞서 열거한 국내 동호인복식경기에서 사용되는 모든 점수 산정 방식에 대한 직접적인 비교가 없었다. 본 연구에서는 현재 국내 동호인복식경기에서 사용되는 여러 가지 점수 산정 방식에 따른 승패의 확률을 체계적인 확률 이론을 적용하여 정량적으로 분석하고, 그 결과를 몇 개의 구체적인 사례에 적용하여 직접적인 비교를 수행하고자 한다. 또한 부수적으로 확률에 대한 이해를 통하여 경기 능력 향상에 간접적인 도움을 주고자 한다.
먼저, 국내의 동호인 복식 경기에서 사용되는 점수 산정 방식을 살펴보면 다음의 몇 가지로 요약될 수 있다. 첫째는 전통적 점수 산정 방식으로 한 게임을 얻기 위해서 6점 중 4점을 먼저 따야 하되 3-3(40:40)부터는 2점 차이로 이겨야 한다, 또한 한 세트를 얻기 위해서는 10게임 중 6게임을 먼저 이겨야 하며 게임 스코어가 5-5인 상황에서는 상대방을 2 게임 차이로 이겨야 한다. 둘째는 6게임 올(6:6)이 되었을 때 1970년 US오픈 테니스대회부터 최초로 채용된 7-점 타이브레이크를 적용하는 방식이다. 셋째는 각 게임을 1999년도부터 도입된 노애드 방식으로 진행하다가 6게임 올이 되었을 때 7-점 타이브레이크를 적용하는 방식이다. 넷째는 국내 동호인 시합에서 관습적으로 채택된 방식으로 각 게임을 노애드 방식으로 진행하되 5게임 올(5-5)이 되었을 경우 7-점 타이브레이크를 적용하는 방식이다. 마지막으로 이의 변형인 1 듀스 노애드 방식으로 경기를 하기도 한다. 이는 진행되는 게임이 3-3이 되면(즉 첫 번째 듀스 상황에서) 5-3으로 이겨야 하고, 만약 4-4가 되면(즉 두 번째 듀스 상황에서) 노애드 방식을 적용하여 그 게임의 승자를 결정한다. 그리고 5게임 올 또는 6게임 올에서는 세트를 결정하는 타이브레이크 게임을 진행한다. 마지막 두 경기 방식은 ITF의 테니스 규칙에서 허용된 점수 산정 방식은 아님을 밝혀 둔다.
이러한 경기 방식에 따른 승패의 확률을 구하기 위해서는 경기 진행 방식을 좀 더 자세히 살펴볼 필요가 있다. 복식은 두 명의 선수가 한 팀을 이루게 된다. 두 팀 중 한 팀이 서브권을 획득하면 그 중 한 선수가 서브 게임을 시작하게 된다. 먼저 서브권을 획득한 팀을 A팀으로 하고, 그 중 a 선수가 세트의 첫 게임의 서브를 하고 a’ 선수는 셋 째 게임의 서브를 한다고 가정하였다. 서브권이 상대인 B팀으로 넘어가면 그 중 b 선수가 둘 째 게임의 서브를 b’ 선수는 넷 째 게임의 서브를 하게 된다. 즉, a→b→a’→b’의 순서로 서브권이 순환한다. 타이브레이크가 6:6에서 시행되면 서브가 a→(b, b)→(a’, a’)→(b’, b’)→a의 순서로 순환하지만, 타이브레이크가 5:5에서 시행되면 서브가 a’→(b’, b’)→(a, a)→(b, b)→a’의 순서로 순환하게 된다는 점에 유의하여야 한다.
선수 또는 팀 간의 신체적, 정신적, 기술적 및 전술적 능력 등의 복합적 차이가 게임, 세트 및 승부를 결정한다고 볼 수 있다. 즉, 각 선수 또는 팀 사이에서 나타나는 미시적 능력의 차이가 거시적인 실력의 차이를 보여준다고 생각할 수 있다. 확률론적인 관점에서는 5 세트 또는 3 세트인 한 경기를 이길 확률은 한 세트를 이길 확률에 의존한다. 한 세트를 이길 확률은 한 게임을 이길 확률에, 또한 한 게임을 이길 확률은 한 포인트를 이길 확률에 각각 의존한다. 한 포인트를 이길 확률은 전술한 미시적 능력에 의존한다고 가정할 수 있다. 한 포인트는 서브에 의해서 또는 서브 후 상대팀의 리턴에 의해서 또는 서브 및 리턴 후 스트로크, 발리 등의 랠리의 진행에 의해서 결정된다. 이러한 과정을 확률로 표현하여 승패를 예측하는 것은 매우 복잡하고 어려운 일이다. 또한, 서브권자가 한 포인트를 획득할 확률은 서브하는 위치 또는 리턴 하는 선수에 따라 변할 수 있다.
그러나 본 연구의 목적은 정확한 승패 예측 모형을 제안하는 것이 아니라 단지 점수 산정 방식이 승패에 어떠한 영향을 미치는 가를 알아보려는 것이므로 서브권자 x가 하나의 서브권에서 한 포인트를 획득할 확률(서브권 득점 확률: p x )을 기초로 하여 승패의 확률을 계산하는 것으로 충분하다고 여겨진다. 서브권 실점 확률(q x = 1 - p x )은 상대가 그 포인트를 획득할 확률과 같다. 복식 경기에서는 한 팀 당 2 명 씩 모두 4 명의 선수(전술한 a, a’, b, b’)가 참여하므로 최소 각 선수의 서브권 득점 확률인 p a , p a ’, p b , p b ’의 4 개의 입력 인자에 대한 값을 정하여야 한다. 이 값은 각각의 선수의 능력을 표시한 것으로 간주할 수 있으며, 실제로는 지난 경기들의 통계 자료를 분석하여 구해져야 한다. 여기서는 이 값들을 변화시키면서 한 팀을 이룬 선수 간의 실력차 또는 상대팀과의 실력차가 있는 각종 시합 상황에 따라 경기 승패가 어떤 결과로 나오는지 파악하도록 하며, 전술한 점수 산정 방식의 차이가 승패의 확률에 얼마나 기여하는지를 파악하도록 한다.
게임 승패의 확률 게임이 진행될 때, 한 포인트를 얻는 과정은 독립적이며 한 포인트를 얻을 확률은 동일한 분포를 따른다고 가정하였다. 이 때 서브권자 x가 한 게임을 따는 확률인 P x 를 계산하는 방법은 여러 가지가 있을 수 있다. 이 중 분석을 원하는 특정한 결과를 발생시킬 수 있는 모든 포인트 상황의 중복조합을 파악하고 관련된 확률을 더하여 그 결과의 발생 확률을 구하는 전체적 방법이 있지만, 본 연구에서는 한 포인트가 진행될 때마다 그 상황에서 발생할 수 있는 중간 결과들에 대한 확률을 이전 중간 결과들의 확률을 이용하여 갱신(update)하고, 이러한 절차를 순차적으로 반복 적용함으로써, 다양한 게임 결과에 대한 확률을 구하는 반복적 계산을 이용한 상향적(bottom-up) 방법을 사용하였다(Barnett, 2014). 각 선수가 본인의 서브 게임을 획득할 확률이 계산되면 이를 토대로 각 팀이 세트를 획득할 확률, PS를 계산할 수 있다. 여기서도 서브권의 순서가 바뀜에 주의하며 상향적 방법을 사용하도록 하겠다. 계산 방법에 대한 자세한 내용은 다른 논문에서 다루기로 하겠으나 계산 결과는 어떠한 계산 방법을 따르더라도 동일함을 부연해둔다.
A 팀의 a 선수가 첫 서브권을 갖는 게임을 한 예로 설명을 하겠다. 게임이 진행되는 중간에 p(m,n)은 A 팀의 득점 회수가 m이고 실점 회수가 n일 때의 확률을 나타내기로 한다. 첫 번째 포인트가 끝났을 때, A팀 대 B팀의 스코어는 1-0 또는 0-1이 유일한 가능성이며, 발생 확률은 각각 p a, qa이다. 두 번째 포인트가 종료되었을 때 발생 할 수 있는 스코어는 2-0, 0-2, 또는 1-1이며, 2-0은 1-0 상황에서 A 팀이 한 점을 더 얻어야만 가능함으로 그 확률은 p(2,0) = p(1,0) × p a, 0-2는 0-1 상황에서 A 팀이 한 점을 더 잃어a 이다. 1-1은 1-0 상황에서 A 팀이 실점하거나, 0-1 상황에서 A 팀이 득점하는 경우에만 발생하므로, 이 둘은 배반 사건이다. 1-1 스코어가 발생할 확률은 이 두 가지 배반사건의 확률의 합, 즉 p(1,1) = p(1,0) × q a + p(0,1) × pa이다. 한 포인트가 더 진행 되었을 때는 3-0, 2-1, 1-2, 0-3 총 4 가지의 중간 스코어가 발생 할 수 있는데, 전술한 방법을 계속 적용하여 각각의 확률은 계산할 수 있다. 이와 같은 절차를 통하여 일반적으로 어느 시점까지는 서로 다른 중간 스코어의 개수가 증가하면서 계산할 확률의 개수 또한 늘어나지만, 그 이후에는 게임이 종료되는 상황이 계속 발생하면서 오히려 작업의 양이 줄어들게 된다. 예컨대, 4 개의 포인트가 끝났을 때 가능한 스코어는 4-0, 0-4 (게임 종료)와 3-1, 1-3, 2-2인 반면, 6 개 포인트가 끝났을 때 발생 할 수 있는 스코어는 4-2, 2-4 (게임 종료)와 3-3 뿐이다. 이 방법의 장점은 각 중간 단계에서의 확률 계산이 오직 전 단계에서의 확률과 그 단계에서의 한 포인트를 이기고 질 확률만을 필요로 하기 때문에 게임 종료 스코어(4-0, 4-1, 4-2 등)에 대한 확률 또한 첫 번째 방법에 비하여 경우의 수, 중복조합 등을 고려할 필요 없이 쉽게 구할 수 있다는 점을 들 수 있다. 반면 단점으로는 단계적으로 결과를 구하기 때문에, 중복 조합을 사용하는 방법과는 달리 특정한 게임 종료 스코어의 확률만을 처음부터 한꺼번에 계산하는 것이 불가능하다는 것이다. 물론, 두 해석 방법은 다르지만 모든 게임 스코어에 대한 확률은 같아야 하며 이는 이미 검증 과정을 거친 상태이다.
본 논문에서는 다양한 경기 진행 방식에 대한 비교가 관건인 만큼, 이 시점에서 노애드, 1 듀스 노애드, 또는 듀스 방식이 적용되는 게임에 관한 확률 계산에 대하여 추가적인 설명이 필요하다. 이 세 가지 방식의 차이는 진행되는 게임의 중간 스코어가 3-3, 즉 듀스가 됐을 경우 승자를 가리는 방법이 다르므로 게임 종료에 대한 확률 계산 방법에 대하여 논하겠다. 먼저 노애드 방식이 적용되는 경우를 고려해보자. 3-3 상황에서 서브권을 가진 복식 조가 그 게임을 이길 확률은 3-3 스코어가 될 확률과 노애드 포인트를 딸 확률의 곱인 조건부 확률의 경우이므로 p a (NA) = p a (3,3) × p a 이고 NA는 노애드 방식임을 표시한다. 다음은 1 듀스 노애드 방식에서 중간 스코어가 3-3이 되었을 때, 그 이후의 결과에 대한 확률 계산에 대하여 설명하고자 한다. 이 상황에서 경기가 종료되는 경로는 두 가지가 있는데, 첫째는 한 팀이 두 포인트를 연속으로 이기는 것이고, 둘째는 두 팀이 한 포인트씩 주고받은 후, 다시 듀스가 된 상황에서 마지막 포인트를 따면 게임을 이기는 것이다. 따라서 1 듀스 노애드 상황을 통하여 A 팀이 게임을 이길 확률은 p a (1DNA) = p a (3,3) × p a × p a + p(4,4) × p a 이다. 마지막으로 듀스 방식에서 중간 스코어가 3-3이 되었을 때는 한 팀이 두 점을 연속으로 획득할 때까지 계속되기 때문에 이론상 게임이 무한하게 진행 될 수 있다는 점에서 노애드, 1 듀스 노애드 방식과 다르다고 할 수 있겠다. 서브권자 a가 서브 하는 게임을 가정하여, A 팀이 3-3 상황을 거쳐 이 게임을 이길 확률은 여러 가지 시나리오의 확률들의 합이 무한 등비급수로 표시되기 때문에 간단한 식으로 표시된다.
이러한 방법으로 각 선수가 서브권을 가졌을 때 특정 점수차로 그 게임을 얻을 확률이 구해지면 이들을 모두 합하여 그 복식 조가 그 게임을 이길 확률을 최종적으로 구하게 된다. 즉 a 선수가 그 게임을 딸 확률은 다음과 같이 표현된다.
여기서 p a (rule)는 3-3 즉, 듀스 상황에서 승부를 결정짓는 방법에 따른 확률이다. P a 는 러브로 이길 확률과 한 점만 내주고 이길 확률과 두 점만 내주고 이길 확률과 듀스 상황을 거쳐 이길 확률의 합에 해당 된다. 복식 경기에서는 네 선수가 번갈아 서비스 권을 갖게 됨으로 이러한 절차를 통하여 계산해야 하는 게임 결과에 관련된 확률은 각 선수가 서브권에서 그 게임을 이길 확률 P a , P a ’, P b , P b ’ 의 네 가지가 된다. 물론 서브권자가 본인의 서비스 게임을 잃을 확률은 Q x = 1 - P x 이다
세트를 결정하는 방식은 전통적 듀스 방식, 6-6에서 타이브레이크를 하는 방식, 그리고 국내 동호인 대회에서 통용되는 5 올 타이브레이크 방식의 세 가지가 있다. 세트 결과에 대한 확률을 구하는 방법도 중복 조합을 이용한 전체적 방법 대신에 한 게임이 진행될 때마다 그 상황에서 발생할 수 있는 중간 결과들에 대한 확률을 이전 결과들의 확률을 이용하여 갱신하고 이러한 절차를 순차적으로 반복 적용함으로써, 다양한 게임 결과에 대한 확률을 구하는 반복적 계산을 이용한 상향적 방법을 사용하였다. 어떠한 계산 방식을 취하더라도 세트 승패의 확률은 동일하게 계산된다. 여기서도 간단한 예를 통하여 설명하도록 하겠다. 다만 게임이 진행되며 서브권이 바뀜에 따라 입력하는 확률도 바뀜에 유의하여야 한다. 먼저 서브를 시작한 A 팀의 얻은 게임수를 m, 잃은 게임수를 n이라하고 이러한 중간 스코어가 발생할 확률을 P(m,n)이라 하자. 정해진 대로, a가 서브하는 첫 게임이 끝났을 때 가능한 중간 스코어는 1-0 또는 0-1이고 각각의 확률은 P(1,0) = P a , P(0,1) = Q a = 1 - P a 이다. 선수 b가 서브하는 두 번째 게임이 종료된 상황에서 가능한 중간 스코어는 2-0, 1-1, 0-2 셋이다. 규정에 따르면 스코어는 경기 중 서브권자의 획득 게임 수를 먼저 부르지만, 여기서는 편의상 첫 서브를 한 A 팀의 획득 게임 수를 앞에 놓았다. 서브권자가 바뀜에 유의하면 P(2,0)는 P(1,0) × Q b 이고,P(1,1)는 P(1,0) × P b + P(0,1) × Q b 이고, P(0,2)는 P(0,1) × P b 이다. 그리고 이와 같은 과정을 계속 반복적으로 수행하다 보면 어느 시점에서 자동적으로 6-0, 6-1, 6-2, 6-3, 6-4의 스코어로 (A 팀이 이길 경우) 또는 0-6, 1-6, 2-6, 3-6, 4-6의 스코어로 (B 팀이 이길 경우) 세트가 종료 될 확률이 각각 산출된다.
게임 스코어가 5-5가 되면 3가지 방식이 적용된다. 첫째는 전통적 방식으로 7-5(5-7) 또는 그 이상에서 2 게임 차이로 승리(패배)를 결정 하는 것이고, 둘째는 6-6이 되었을 때 7점 타이브레이크를 실시하여 승패를 결정하는 것이고, 셋째는 국내에서 통용되는 방식으로 5-5에서 바로 7점 타이브레이크를 실시하여 승패를 결정하는 것이다.
듀스 게임 방식이 적용되는 경우, 게임 스코어가 6-6이 되는 확률 P(6,6)을 먼저 계산하고, 그 이후에 A 팀의 승리로 세트가 끝날 수 있는 시나리오는 a와 b의 서비스 게임을 A가 모두 이기는 상황, a’과 b’의 서비스 게임을 A가 연속적으로 이기는 상황의 두 가지가 있다. 두 경우 모두 원칙적으로는 경기가 무한하게 진행될 수 있으므로 각 확률의 값은 수렴되는 무한 등비급수의 합으로 표현이 가능하다. 결과적으로 6-6 상황에서 A 팀이 세트를 이길 확률은 P(Deuce) = P(6,6) × PDD이고, PDD는 6-6 스코어가 되었을 때 A 팀이 그 이후의 경기 부분에서 두 게임을 연속으로 이길 확률이다.
5-5 상황에서는 점수 산정 방식에 따라 바로 타이브레이크가 적용되거나 6-6 상황이 될 때 타이브레이크가 적용된다. 각각의 경우, a’ 선수와 a 선수의 서브권으로 타이브레이크가 시작된다는 점에만 유의하면 전술한 상향적 계산 방법으로 타이브레이크의 승패에 관한 확률을 쉽게 계산할 수 있다. 좀 더 자세한 설명은 별도의 논문에 발표할 예정이다. A팀이 5-5에서와 6-6에서 타이브레이크를 이길 확률을 각각 P TB5와 P TB6라고 할 때, 최종적으로 그 세트를 이길 확률은 5 올 타이브레이크 방식이 적용되면 P(5,5) × P TB5이고 6 올 타이브레이크 방식이 적용되면 P(7,5) + P(6,6) × P TB6로 주어진다.
이러한 모든 해석 결과를 토대로 A 팀이 한 세트를 이길 확률 P S (A)는 세트가 A 팀의 승리로 종결되는 모든 스코어의 발생 확률을 합산하여 구하면 된다.
여기서 P(rule)은 경기 방식에 따른 5-5 이후에 A 팀의 승리로 경기가 종료되는 확률이며, 전통적 듀스 방식의 경우는 P(7,5) + P(Duece)이고, 6-6 타이브레이크 방식의 경우는 P(7,5) + P(TB6), 5-5 타이브레이크 방식의 경우는 P(TB5)가 된다.
이미 설명한 바와 같이 여기서 제시된 계산 방법은 각 게임의 결과에 대한 확률 분석을 먼저 수행하고, 이를 토대로 세트의 결과에 대한 확률 분석을 하는 특성상 단순히 특정한 세트를 이길 확률뿐만 아니라, 특정한 스코어로 게임 또는 세트가 종결될 확률을 중간 과정에서 계산함으로 보다 심도 있는 세부적인 정보의 추출이 가능하다는 장점을 지니고 있다. 즉 점수 산정 방식의 차이가 승패의 향방에 미치는 영향이나 승패에서 특정한 게임 스코어가 발생할 확률이 각각 무엇인지 까지도 정확히 계산할 수 있다.
앞 절에서 고려한 테니스 복식 경기에서의 점수 산정 방식(즉 승패를 결정하는 방식)이 승부에 미치는 영향을 살펴보기 위하여, 게임을 결정하는 방식 3 가지에 따른 확률값을 계산하고, 동호인들이 주로 사용하는 세트를 결정하는 5 가지 방식에 대하여 분석을 시도하였다. 두 팀 A와 B가 복식 경기를 할 때, 각 팀의 실력을 각 선수들의 서브권 득점 확률의 평균이라고 가정해 보겠다. 본 연구에서 게임의 승패는 상대의 실력과 무관하게 계산되지만, 세트의 승패는 복식에 참여한 4명의 선수의 실력에 의존한다. 따라서 계산하여야 할 경우의 수가 너무 많으므로 몇 가지 흥미로운 경우에 대해서만 계산하고 분석을 시도하였다.
먼저, 한 선수가 서브권을 갖고 있을 때 그 포인트를 딸 확률이 p인 경우 해당 게임을 얻을 평균 확률 P를 계산해 보았다. 게임을 진행하는 방식은 세 가지가 가능한데, 전통적 방식(즉 듀스 방식)과 노애드 방식과 1 듀스 노애드 방식이다. 듀스를 통하지 않고 한 게임을 따는 방법은 4-0(러브 게임), 4-1(게임:15), 4-2(게임:30)이며 어떤 방식을 따르던 그 확률은 동일하다. 따라서 듀스 상황에서 점수 산정 방식에 따라 게임 획득 확률이 변하게 된다. <그림 1>에서 보인 것처럼 p < 0.5인 경우에는 게임 획득 확률이 서브권 득점 확률보다 낮게 나타난다. 그 후, 0.35 < p < 0.65인 경우에 게임 획득 확률이 크게 증가한다. p > 0.5이면 서브권에서 득점 확률보다 게임 획득 확률보다 커진다. 이와 같은 현상은 한 게임의 여러 포인트의 향방이 누적된 결과이기 때문이다. 점수 산정 방식에 따른 확률은 p > 0.5일 때, 듀스 방식(Deuce), 1 듀스 노애드 방식(1D-NA), 노애드 방식(NA)의 순서로 큼을 알 수 있다. 즉, 노애드 방식이 서브권자에게 가장 불리하게 나타난다. 특히 p = 0.65일 때, 그 차이가 가장 커서 P(Deuce)는 약 83.0%이지만 P(NA)은 약 80.0%로 그 차이가 약 3.0%P가 된다. 물론, 확률의 대칭성에 따라 p < 0.5인 경우는 반대로 됨을 확인할 수 있다.
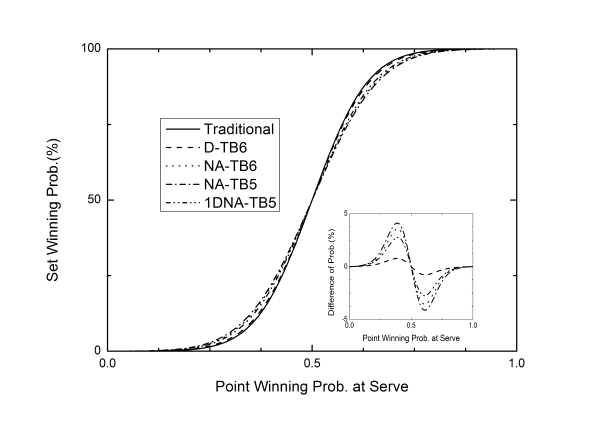
먼저 한 팀이 동일한 실력을 지닌 두 선수로 이루어져 있다고 가정하면, 이는 기초적인 단식의 확률 모형의 결과와 같아진다. 리시브 팀의 각 선수의 서브권 득점 확률을 pb = pb’ = 0.5로 고정하고 먼저 서브한 팀의 각 선수의 서브권 득점 확률 p = pa = pa’을 0에서 1까지 변화시키며 세트 획득 확률을 계산하였다. <그림 2>에서 보인 것처럼 p > 0.5인 경우에 전통적 방식(D-D), 듀스-6올 타이브레이크 방식(D-TB6), 현행 국제 대회 방식인 노애드-6올 타이브레이크 방식(NA-TB6), 1듀스 노애드-5올 타이브레이크 방식(1DNA-TB5), 현행 국내 동호인 대회 방식인 노애드-5올 타이브레이크 방식(NA-TB5)의 순으로 세트 획득 확률이 낮아지며, p < 0.5인 경우는 반대의 순서가 된다. 이 경우, 0.39 < p < 0.61 구간에서 세트 획득 확률이 가파르게 증가함을 보여 준다. 또한 p = 0.39와 p = 0.61에서 각 점수 산정 방식에 따른 확률 차이가 가장 크게 나타났다. 예로, p = 0.61일 때, 전통적 방식, 현행 국제 경기 방식, 그리고 국내 동호인 대회 방식에서의 세트 획득 확률이 순서대로 84.3%, 80.7%, 80.1%으로 나타난다.
이제 조금 다른 상황을 다뤄 보기로 하겠다. 첫 서브권을 지닌 A 팀의 선수들이 서브권 득점 확률을 각각 p a = 0.6, p a ’ = 0.5이라 하고, 상대방 B 팀 선수들의 확률을 p b = p b ’ = 0.5 이라 하면, 실력이 약간 차이 나는 두 팀이 복식 단 세트 경기를 진행한다고 볼 수 있다. 실제 경기에서는 두 팀 중에서 먼저 서브를 하는 팀을 동전 던지기 등의 추첨 방식을 통하여 결정하므로 어느 팀이 먼저 서브권을 갖는 가는 50%의 확률로 나타난다고 볼 수 있다. <표 1>에서 보인 것처럼 A 팀이 강하므로, 점수 산정 방식이나 서브 순서에 무관하게 승리하게 되고 그 확률은 최저 약 62%에서 최고 약 69%로 나타난다. 서브 순서가 정해진 각각의 경우에 점수 산정 방식에 따른 승률의 차이는 약 3%P 정도이다. 또한, 미시적 실력이 강한 선수와 약한 선수가 한 팀을 이룬 경우는 강한 선수가 먼저 서브를 넣을 때 승률이 높아짐을 확인할 수 있다. 다른 값의 p b 를 사용하면 p a > p b 이어야 승률이 50%를 넘어 가며, 앞의 결과와 비슷한 경향을 보임을 부연해둔다. 즉, 실력이 약간이라도 높은 팀이 실력이 약한 팀보다 세트를 이길 확률이 현저히 높음을 알 수 있으며. 그 확률 값은 점수 산정 방식이나 서브의 순서에도 적지 않은 영향을 받는 것을 볼 수 있다.
| p a | p a ’ | p b | p b’ |
P
s
D-D |
P
s
D-TB6 |
P
s
NA-TB6 |
P
s
NA-TB5 |
P
s
1DNA-TB5 |
|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.5 | 0.5 | 0.5 | 0.690506 | 0.681320 | 0.663037 | 0.672932 | 0.682372 |
| 0.5 | 0.6 | 0.5 | 0.5 | 0.653742 | 0.654031 | 0.638588 | 0.621923 | 0.628406 |
| 0.5 | 0.5 | 0.5 | 0.6 | 0.346258 | 0.348115 | 0.363569 | 0.373783 | 0.367310 |
| 0.5 | 0.5 | 0.6 | 0.5 | 0.309494 | 0.316652 | 0.334901 | 0.331210 | 0.321736 |
미시적 실력이 약간이라도 높은 팀이 실력이 약한 팀보다 이길 확률이 확연하게 높음을 알 수 있다. 그러나 점수 산정 방식이나 서브의 순서에도 확률값이 영향을 받는다. 여기서는 a→b→a’→b’의 순서로 서브권을 지닌다고 가정하였다. 여기서 D-D는 전통적 방식을 D-TB6는 듀스 게임과 6 올 타이브레이크 방식을 NA-TB6는 노애드 게임과 6 올 타이브레이크 방식(현 국제 대회에서 주로 사용)을 NA-TB5는 노애드 게임과 5 올 타이브레이크 방식(현 국내 동호인 대회에서 주로 사용)을 1DNA-TB5는 듀스가 두 번 될 때의 노애드 게임과 5 올 타이브레이크 방식을 각각 의미한다.
다음에 미시적 실력이 비슷하다고 여겨지는 두 팀 간의 승패확률을 고려해 보았다(p a + p a ’ = p b + p b ’). 이 때 한 팀은 강한 선수와 약한 선수로 이루어져 있고) 다른 팀은 비슷한 실력을 가진 선수로 이루어져 있다고 가정하였다. 계산할 경우의 수가 너무 많으므로 점수 산정 방식의 특성을 보여 줄 수 있고 복식 경기에 대한 이해에 도움이 될 만한 몇 가지에 한정하였다. 여기서 실력이 같은 팀의 서브권 득점 확률을 0.4에서 0.7까지 변화시키면서 세트 획득 확률을 계산하여 <표 2>에 정리 하였다. 실력이 다른 팀에서는 반드시 강한 선수가 약한 선수보다 먼저 서브를 하여야 세트 득점 확률이 높아짐을 확인할 수 있다. 이 때, 두 선수 간의 실력차가 크면 서브의 순서가 승률에 크게 영향을 줌을 알 수 있다. 비슷한 실력을 지닌 팀의 각 선수의 서브권 득점 확률이 50% 미만이면 강한 선수와 약한 선수로 이루어진 팀의 승률이 높게 나타났으나, 50% 이상이 되면 비슷한 실력의 선수로 이루어진 팀의 승률이 높아지는 결과가 나타났다. 계산한 경우만을 고려하면, 점수 산정 방식도 승률에 영향을 줌을 알 수 있다.
현재 프로 복식 경기에서 주로 사용되는 방식은 노애드-6올 타이브레이크 방식이고 국내 동호인 시합에서 사용되는 방식은 노애드-5올 타이브레이크이다. 실제 시합 상황이라면 <표 2>에서 볼드체로 표시된 것처럼 승률을 높이기 위해서는 서브권 득점 확률이 큰 선수가 먼저 서브를 하게 될 것이다. 이때, A 팀에게 p a > p a ’이면 5-5 타이브레이크가 유리하고 p a = p a ’이면 6-6 타이브레이크가 상대적으로 유리하다. 이는 첫 서브권자는 한 번만 서브하고, 그 다음부터는 두 번씩 서브하는 타이브레이크 게임의 특성 때문이다(Pollard, 2005).
| p a | p a ’ | p b | p b’ |
P
s
D-D |
P
s
D-TB6 |
P
s
NA-TB6 |
P
s
NA-TB5 |
P
s
1DNA-TB5 |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.3 | 0.4 | 0.4 | 0.855153 | 0.837964 | 0.811982 | 0.833884 | 0.847351 |
| 0.3 | 0.5 | 0.4 | 0.4 | 0.817643 | 0.806839 | 0.779357 | 0.760979 | 0.773986 |
| 0.4 | 0.4 | 0.5 | 0.3 | 0.392395 | 0.408006 | 0.430563 | 0.422994 | 0.412173 |
| 0.4 | 0.4 | 0.3 | 0.5 | 0.465077 | 0.469557 | 0.488952 | 0.505175 | 0.498778 |
| 0.6 | 0.4 | 0.5 | 0.5 | 0.540676 | 0.529916 | 0.526336 | 0.555008 | 0.558717 |
| 0.4 | 0.6 | 0.5 | 0.5 | 0.459324 | 0.470084 | 0.473664 | 0.444992 | 0.441283 |
| 0.5 | 0.5 | 0.6 | 0.4 | 0.459324 | 0.465370 | 0.469000 | 0.454321 | 0.450662 |
| 0.5 | 0.5 | 0.4 | 0.6 | 0.540676 | 0.534630 | 0.531000 | 0.545679 | 0.549338 |
| 0.7 | 0.3 | 0.5 | 0.5 | 0.576436 | 0.555977 | 0.551098 | 0.607488 | 0.613146 |
| 0.3 | 0.7 | 0.5 | 0.5 | 0.423564 | 0.444023 | 0.448902 | 0.392512 | 0.386854 |
| 0.5 | 0.5 | 0.7 | 0.3 | 0.423564 | 0.433306 | 0.438399 | 0.413518 | 0.408104 |
| 0.5 | 0.5 | 0.3 | 0.7 | 0.576436 | 0.566694 | 0.561601 | 0.586482 | 0.591896 |
| 0.7 | 0.5 | 0.6 | 0.6 | 0.465077 | 0.463992 | 0.483568 | 0.515659 | 0.509452 |
| 0.5 | 0.7 | 0.6 | 0.6 | 0.392395 | 0.414760 | 0.436968 | 0.412984 | 0.402119 |
| 0.6 | 0.6 | 0.7 | 0.5 | 0.534923 | 0.530443 | 0.511048 | 0.494825 | 0.501222 |
| 0.6 | 0.6 | 0.5 | 0.7 | 0.607605 | 0.591994 | 0.569437 | 0.577006 | 0.587827 |
| 0.8 | 0.4 | 0.6 | 0.6 | 0.334624 | 0.341396 | 0.396386 | 0.464526 | 0.441562 |
| 0.4 | 0.8 | 0.6 | 0.6 | 0.223843 | 0.266157 | 0.318290 | 0.283789 | 0.259376 |
| 0.6 | 0.6 | 0.8 | 0.4 | 0.665376 | 0.649276 | 0.593725 | 0.558181 | 0.581223 |
| 0.6 | 0.6 | 0.4 | 0.8 | 0.776157 | 0.745461 | 0.693924 | 0.697651 | 0.722825 |
| 0.8 | 0.6 | 0.7 | 0.7 | 0.395034 | 0.419530 | 0.441693 | 0.476679 | 0.466167 |
| 0.6 | 0.8 | 0.7 | 0.7 | 0.346729 | 0.394998 | 0.412733 | 0.393786 | 0.383716 |
| 0.7 | 0.7 | 0.8 | 0.6 | 0.604966 | 0.568609 | 0.547982 | 0.538188 | 0.549481 |
| 0.7 | 0.7 | 0.6 | 0.8 | 0.653271 | 0.617444 | 0.598382 | 0.592380 | 0.601899 |
각 선수들의 서브권 득점 확률이 주어졌을 때, 먼저 서브권을 지닌 팀의 세트 획득 확률이 점수 산정 방식에 따라 달라짐을 알 수 있다. 여기서는 a→b→a’→b’의 순서로 서브권을 지닌다고 가정하였다. 여기서 D-D는 전통적 방식을 D-TB6는 듀스 게임과 6 올 타이브레이크 방식을 NA-TB6는 노애드 게임과 6 올 타이브레이크 방식(현 국제 대회에서 주로 사용)을 NA-TB5는 노애드 게임과 5 올 타이브레이크 방식(현 국내 동호인 대회에서 주로 사용)을 1DNA-TB5는 듀스가 두 번 될 때의 노애드 게임과 5 올 타이브레이크 방식을 각각 의미한다.
본 연구에서는 점수의 발생이 독립적이고 동등한 분포를 갖는다는 가정을 하였으나, 실제 경기를 분석한 선행 연구 결과를 살펴보고자 한다. Knight와 O’Donoghue는 2008년과 2009년의 4개 Grand Slam의 남자 단식 528 매치를 분석하여 브레이크 포인트에서는 리시버의 득점확률이 0.38±0.10에서 0.42±0.23으로 증가하였다고 보고하였다(Knight & O’Donoghue, 2012). 또한 Klaassen과 Magnus는 1992년에서 1995년의 윔블던 단식의 481 매치의 86,298 포인트를 분석하여 점수가 독립적이고 동등한 분포에서 약간 벗어남을 보였다(Klaassen & Magnus, 2001). 이는 포인트 간에 선수들의 심리적 효과가 작용함을 의미한다고 생각하였다. Newton과 Aslam은 2002년 U. S. Open 남녀 단식 경기를 분석하여 점수가 독립적이고 동등한 분포에서 약간 벗어남을 확인하였으나 대체적으로 점수의 분포가 독립적이고 동등하다고 가정하여도 경기의 승패를 확률 67% 정도로 맞출 수 있다고 보고 하였다(Newton & Aslam, 2006). 따라서 실전에서는 노애드 상황처럼 승부에 중요한 영향을 주는 상황이 있는데, 이때는 집중력을 발휘하거나 전략, 전술적인 고려를 통하여 승률을 높이는 능력이 선수들에게 필요하다(Pollard & Pollard, 2007a & 2007b; Barnett, 2012).
한 선수의 실력을 이야기할 때, 단식의 경우는 서브권 득점 확률이나 전체 승률 중 무엇을 선택하여도 무방하다고 생각된다. 프로 단식의 경우 테니스 프로 협회(ATP)는 남자 프로 선수 관한 여자 테니스 프로 협회(WTA)는 여자 프로 선수의 경기의 통계 자료를 제공하고 있다(ATP statistics; WTA statistics). 본 연구의 결과를 역으로 이용하면 남자의 경우 서브 게임을 따는 확률이 높게는 P=0.93이므로 p=0.75 정도로 추산 된다. 여자의 경우 서브 게임을 따는 확률이 높게는 P=0.82이므로 p=0.65 정도로 추산 된다. 본 연구에서는 p a > 0.5, p a > p b 이면, P A S > P a > P b >의 결과를 얻었다. 즉, 미시적 실력의 척도로 생각한 서브권 득점 확률이 50% 이상이 되면, 게임을 획득할 확률이 50% 이상이 된다. 이는 앞에서 언급한 획득 포인트의 누적 효과에 기인하기 때문이다. 그러나 세트를 획득하기 위해서는 당연히 p a > p b 이어야 한다.
복식의 경우, 한 팀의 실력이 두 선수의 서브권 득점율의 합(p x + p x ’) 또는 그 평균으로 표현될 수 있다고 생각하기 쉽다. 그러나 p a + p a ’ = p b + p b ’인 경우, 즉 미시적 평균 실력이 같은 경우에도, 그 값과 파트너 간의 실력차에 따라 세트 획득 확률이 다양하게 나타난다. 본 연구에서는 복식 경기에서의 득점 과정이 팀 내 두 선수간의 협업에 의해서도 이루어지는 특성을 간과한 것이므로 추후에 좀 더 자세한 연구가 필요하다. 그러나 이전까지 알려진 세트의 승률이나 게임 획득 확률이 각기 다른 4 선수가 복식을 한다면, 본 연구에서 사용한 각 선수의 서브권 득점 확률로 승패를 예측하는 것이 무난 할 것으로 예상된다.
한 선수가 서브권을 가졌을 때 득점 하는 방법은 제 1 서브가 성공하면 에이스 또는 서브 포인트를 얻거나 리턴 된 공을 효과적으로 처리하거나 랠리가 이루어진 후 득점 하는 과정과 제 1 서브가 폴트가 된 경우에는 제 2 서브를 성공하여 전술한 일련의 과정으로 나눌 수 있다. 일반적으로 선수들은 강력하지만 성공률이 낮은 서브를 제 1 서브로 안정되지만 위력이 약한 서브를 제 2 서브로 사용하여 시합을 하고 있다. 이 두 서브를 확률론에 따라 효과적으로 사용하는 방법에 관하여 이미 여러 논문에서 다루고 있다(Barnett, 2012; Barnett et al., 2012, George, 1973; Spanias & Knottenbelt, 2012). 이것은 상대 선수의 리턴 능력을 감안해야 함을 의미한다고도 볼 수 있다. 따라서 서브에 의한 득점 과정뿐만 아니라 리턴에 의한 실점 과정을 확률 계산 모형에 포함시키는 향후 연구가 필요하다고 볼 수 있다(Knottenbelt et al., 2012).
테니스 복식 경기의 점수 산정 방식은 전통적 방식조차 불공정성이 내재함이 알려져 있다. 이미 이를 개선하기 위한 연구가 있어 왔지만 아직 ITF의 경기 규정에 반영되고 있지는 않다(Brown et al., 2008; Pollard, 2005; Pollard, 2007; Pollard & Noble, 2003a & 2003b). 국내 동호인 대회에서 경기 시간의 단축이 5-5 타이브레이크를 도입한 주된 이유라면 ITF 규정에서 허용된 4 게임 방식이나 노 서비스 레트 게임을 사용하는 것이 국제 교류 등을 감안하면 바람직하다고 여겨진다(ITF rule).
테니스 복식 경기에서의 점수 산정 방식(즉 승패를 결정하는 방식)이 승부에 미치는 영향을 살펴보았다. 국제 테니스 연맹 경기 규정 뿐 아니라 국내 동호인이 사용하는 점수 산정 방식까지도 고려하여, 한 선수의 서브권 득점 확률이 독립적이며 동등한 분포를 갖는다고 가정하고 상향적 방식에 따라 게임 획득 확률 및 세트 획득 확률을 계산하였다. 따라서 게임을 결정하는 방식 3 가지에 따른 확률을 계산하고, 국내 동호인들이 주로 사용하는 세트를 결정하는 3 가지 방식을 고려하여 모두 5 가지 경우의 점수 산정 방식에 따른 한 세트에서의 승패의 확률을 계산하여 비교하였다.
비록 대표적인 몇 가지 경우에 대한 결과이지만 동일한 팀 구성 및 서브 순서의 가정하에서도 어떠한 점수 산정 방식을 적용하는 가에 따라 세트의 승패 확률이 7-8%P까지 차이가 남을 알 수 있었다. 특히, 특정한 선수의 조합에서는 국내 동호인 시합에서 사용하는 5 올 타이브레이크 방식을 사용하면 전통적 방식에 의한 승률과 차이가 크게 나므로 승패의 결과가 왜곡될 수 있음을 의미한다. 부수적으로, 승률을 높이기 위한 바람직한 팀의 구성이나 서비스 순서 등에 대한 정보를 유추할 수 있었다.
이러한 본 연구의 결과는 본 논문에서 다룬 다양한 경기 방식의 공정성을 객관적인 차원에서 평가할 수 있는 기초적인 근거를 제공하며, 이는 주어진 상황에 따른 적절한 경기 방식의 선정, 그리고 한 걸음 더나가 기존 방식의 개선책 연구에도 도움이 될 것으로 기대된다. 물론 결과의 정확도를 향상시키기 위해서는 본 연구에 적용된 모형을 보다 확장하여 한 포인트의 향방을 결정짓는 다양한 요소들(제1, 제2 서브 능력, 리턴 능력 등)을 적절히 반영하는 서브권 득점 확률 모형, 그리고 게임 도중의 스코어를 반영하는 적응 모형의 개발 등도 병행되어야 할 것이다.
이 논문은 2008학년도(박동욱) 및 2014학년도(한원근) 홍익대학교 학술연구진흥비에 의하여 일부 지원되었음.
A recursive approach to modelling the amount of time played in a tennis match () (2014) Barnett, T. (2014). A recursive approach to modelling the amount of time played in a tennis match. www.strategicgames.com.au. , www.strategicgames.com.au
, Barnett, T., & Clarke., S. (2002). , Using Microsoft Excel to model a tennis match, . 6th Conference on Mathematics & Computers in Sport. Bond University, Queensland, Australia., , 2002, Using Microsoft Excel to model a tennis match , 6th Conference on Mathematics & Computers in Sport, Bond University, Queensland, Australia
, Brown, A., Barnett, T., Pollard, G. H., & Pollard, G. N. (2008). The characteristics of various men's tennis doubles scoring systems. , Proceedings of the Ninth Australian Conference on Mathematics & Computers in Sport, . , , 2008, The characteristics of various men's tennis doubles scoring systems, Proceedings of the Ninth Australian Conference on Mathematics & Computers in Sport
Tennis Science & Technology (, et al., 3rd. ed, , et al., ) (2007) International Tennis Federation Pollard, G., et al. (2007). Some alternative men’s doubles scoring systems. Tennis Science & Technology(3rd. ed., S. Miller and J. Capel Davies). International Tennis Federation, 301-309. , Some alternative men’s doubles scoring systems, pp. 301-309
Tennis Science & Technology (, et al., , 2nd. ed, ) (2003a) International Tennis Federation Pollard, G., & Noble, K. (2003a). A new tiebreak game with four proposed applications. Tennis Science & Technology(2nd. ed., S. Miller). International Tennis Federation, 317-324. , A new tiebreak game with four proposed applications, pp. 317-324
Tennis Science & Technology (, et al., , 2nd. ed, ) (2003b) International Tennis Federation Pollard, G., & Noble, K. (2003b). A solution to the unfairness of tiebreak tennis doubles. Tennis Science & Technology(2nd. ed., S. Miller). International Tennis Federation, 325-332. , A solution to the unfairness of tiebreak tennis doubles, pp. 325-332
Tennis Science & Technology (, Pollard, G., 3rd. ed, , et al., ) (2007a) International Tennis Federation Pollard, G., & Pollard, G. (2007a). Importances 1: the most important sets in a match, and the most important points in a game of tennis. Tennis Science & Technology (3rd. ed., S. Miller & J. Capel-Davies). International Tennis Federation, 281-292. , Importances 1: the most important sets in a match, and the most important points in a game of tennis, pp. 281-292
Tennis Science & Technology (, et al., , 3rd ed, , et al., ) (2007b) International Tennis Federation Pollard, G., & Pollard, G. (2007b). Importances 2: the most important sets in a tiebreak game, and the most important games in a set. Tennis Science & Technology(3rd ed., S. Miller & J. Capel-Davies). International Tennis Federation, 293-300. , Importances 2: the most important sets in a tiebreak game, and the most important games in a set, pp. 293-300
(ATP Statistics) ATP Statistics, http://www.atpworldtour.com/ , http://www.atpworldtour.com/
(ITF Rule) ITF Rule, http://www.itftennis.com/media/136148/136148.pdf , http://www.itftennis.com/media/136148/136148.pdf
(Tennis People Statistics) Tennis People Statistics, http://www.tennispeople.kr/news/ articleView.html?idxno=18 , http://www.tennispeople.kr/news/ articleView.html?idxno=18
(WTA Statistics) WTA Statistics, http://www.wtatennis.com/ , http://www.wtatennis.com/
