 ISSN : 1598-2920
ISSN : 1598-2920
ⓒ Korea Institute of Sport Science
This study measured the haptic extroperception accuracy, that is, judging one hit position in a hand-held object. Especially, what factors associated the estimation of contact position when the impact is made at the grasped implement by hitting the ball.
Relative frequency and conditional probability based analysis verified that perceivers influenced not only the amount of pressure distinguished impressions by the coefficient of restitution but also the pressure distributions encoded impressions by the distance from the hand to the impact.
Results conformed to previous invariant characteristic on dynamic touch in showing that perceiving the location of the impact of grasped objects, including dominant perceiving selectively modality, is constrained by inertial properties with such success requires appreciating the location of the implement’s center of percussion.
Investigated in this planes captured as a mechanical factor, we would suggest a broader hypothesis for further research into the effects of the rotational inertia related to haptic position accuracy in the hand-held object, and leading to different estimates of system function providing an account of generalization that accommodates of its varied aspects.
본 연구의 목적은 근-감각과 피부감각 정보가 복합적으로 작용하는 촉지각에 기여하는 중요 속성을 알아보는데 있다. 라켓 또는 채와 같은 도구를 손으로 잡고 있는 상황에서 그 도구의 어디에 해당하는 접촉 위치지각이 어떤 자극속성과 깊은 관계가 있는지 알아보고자 한 것이다.
상대 도수 및 조건부 확률을 기반으로 추정된 손에 잡은 도구의 어디에 해당하는 촉지각의 정확성은 (첫째) 동일한 압력의 분포에서 압력의 크기와 관계하였으며 (둘째) 동일한 크기의 압력에서 압력의 분포와도 관계하였다. 그리고 (셋째) 두 자극(압력의 크기와 분포)을 동일한 수준으로 변화하도록 조건화하여 비교한 결과 압력의 크기보다 압력의 분포에 상대적으로 더 안정적인 추정을 보이는 것으로 나타났다. 이러한 결과는 손에 잡은 도구의 위치 지각을 결정하는 양적인 자극 특질이 관성 텐서로 잘 알려진 물리적 속성과 자극에 대한 변이의 추정으로써 잡고 있는 도구에 형성되는 충격중심과 관계가 있는 것으로 사료되었다.
지각(perception)은 주위의 사물과 사건에 대한 정보를 감각 기관을 통해서 획득하는 과정을 말한다(Sherrick & Cholewiak, 1986). 유기체는 다양한 지각(시각, 미각, 청각, 촉각, 후각) 기전을 통해 움직임을 일으키지만 많은 상황에서 시각을 통해 입력되는 정보가 가장 중요하게 작용하는 것으로 알려져 있다(Abernethy, 1990). 그래서 많은 연구들이 시지각(visual perception) 작용에 중점을 두고 있기도 하다. 하지만, 촉지각(haptic) 역시 상황을 인식하는데 그 중요성을 간과할 수는 없다(Grunwald, 2008; Lederman & Klatzky, 2009).
관련된 연구로서, 두 지각체계의 상대적인 우세(dominant modality)를 알아보는 실험에 의하면 물체의 기하학적(geometric) 특질과 같은 공간적(spatial) 정의는 시각이 상대적으로 우세하지만 표면의 거침과 같은 물질적(material) 특질(Ernst & Banks, 2002)과 관계된 상황에서는 촉각이 더 우세(Gescheider, 1974)하였다. 새로운 움직임의 학습은 일반적으로 시각적 정보에 크게 의존하지만 촉각 정보는 추가적인 자기 수용 감각의 정보를 제공해(Bara & Gentaz, 2011), 촉지각 안내(haptic guidance)를 수반할 때 더 빠르고 정확한 학습을 도모할 수 있는(Milot et al., 2010) 것으로 나타났다. 이는 특정 조건, 즉, 시지각 정보가 차단되거나 사전 정보가 없는 상황에서 촉지각이 과제의 적응과 조율에 핵심적으로 작용(Huang et al., 2007)하고 있을 뿐만 아니라, 다양한 상황(i.e., 컵 들기, 망치질 하기, 탁구 또는 골프와 같이 특정 도구를 활용하는 스포츠 등)에서도 중요하게 작용하고 있음을 의미하였다(Crespo & Reinkensmeyer, 2008; Wulf & Toole 1999). 이러한 맥락에서 연구자들은 어떠한 기전(mechanism)이 촉지각 작용에 기저하고 있는지에 대해 더 많은 관심을 기울이게 되었다(Bara et al., 2011; Milot et al., 2010).
구체적으로 행동적 실험과 뇌영상 기법(fMRI)을 통한 연구에 의하면 촉지각 체계가 시각의 복측 경로와 배측 경로 처리 체계(ventral and dorsal pathway)와 같이 “무엇(what)?“의 지각적 기능을 다루는 체계와 ”어디(where)?”의 지각적 안내를 다루는 체계로 구분되며, 두 체계 간의 기능적 분류에 관한 논의를 조직화 하였다(Chan & Newell, 2008; Reed et al., 2005). 촉지각에서 무엇(what) 처리 체계는 물체의 공간적 배열과 표면온도, 질량 등 서로 다른 많은 특질들을 정확하고 빠르게 인식하는 것으로 결정되는 체계이다(Lederman & Klatzky, 2009). 특히, 이 “무엇(what)?”과 관련된 촉지각 정확성 연구들은 지각작용의 기저로서 무게지각(heaviness perception paradigm)과 관련된 물리적 저항과 운동 감각성에 따른 역동적 촉각(dynamic touch, Gibson, 1966; Loomis & Lederman, 1986)에 관심을 기울였다(Turvey & Carello, 1995). 그리고 손에 잡은 도구의 비시각적 촉지각과 관련하여 무게를 추정하게 하는 핵심적 정보로서 관성 텐서(inertia tensor)라는 중요한 물리적 특질이 관여하고 있다는 것을 보고하였다(Turvey, 1996). 그러나 물체를 손으로 잡고 휘두르는 촉지각(dynamic touch) 상황에서 그 타당성이 검증되어온 무게지각의 중요 특질인 관성 텐서는 일반화를 위한 더 다양한 접근이 요구되고 있기도 하였다(Zhu et al., 2013). 왜냐하면, 접촉 지각을 위한 중요한 논쟁 중 다른 분명한 하나는 우리가 어떻게 접촉을 위치(where)로 구분할 수 있는가에 대한 이해를 포함(Lederman & Klatzky, 2009)하고 있기 때문이다.
신체의 어느 부분에서 자극이 이루어졌는가에 대한 결정이 이루어질 때, 다양한 요소 중에서 ‘어디(where)인가?’를 결정하는 것은 표피에 수용된 기계수용기들( 메르켈소체, 마이스너소체, 파치니소체, 루피니소체)의 연합된 민감성에 의해 이루어진다(Barrows, 1915), 특히 진동을 통한 압력의 감지(the cutaneous sense of pressure)가 매우 중요(Witt, 1975; Wolfe et al., 2008)한 것으로 알려져 있는데, 이러한 압력과 관련하여, 역동적 촉각 연구의 시초로 언급 되어 온 Weber (1834, 1978)의 접촉 감각(The Sense of Touch) 연구에 의하면 무게지각의 경우 이를 결정하는 중요한 특질이 손에든 물체를 움직이기 위한 힘으로서의 저항(resistance to forces acting on the object)뿐만 아니라 피부에 가해진 압력(pressure)을 통해서도 이루어진다고 하였다. 특히, Weber (1834, 1978)는 물체의 질량은 압력과 직접적으로 연결되기 때문에 무게 지각은 피부 압력 감각 기능이라고 간주하였고, 나아가서 Stevens & Rubin (1970)은 질량이 동일 할 때 부피가 커짐으로써 낮아지는 밀도(density)는 피부에 적은 압력을 주어 무게지각이 낮아진다는 피부 자극의 중요성을 강조하였다 .
하지만, 진동을 통한 압력이 중요하게 작용하는 촉지각의 어디를 알 수 있느냐의 문제에서는 물리적 자극으로써 압력의 분포가 핵심적인 지각 특질로 역할을 하는지 충분히 다루어지지 못하고 있다(Amazeen & Turvey, 1996). 다시 말해서, 이를 검증 해 볼 필요가 있다(Millar, 1976, 1994)는 궁금증을 일으키고 있다는 것이다. 왜냐하면 어디에 해당하는 손에 잡은 물체의 접촉 위치지각 또한 자극의 크기(amount of pressure)뿐만 아니라 피부 감각 정보를 통한 자극의 분포(pressure distribution)와도 관계(Shaw & Turvey, 1992)가 있을 것이라 짐작되기 때문이다. 나아가서 동일한 수준으로 변화하도록 조건화된 자극의 크기와 분포에서 충돌에 따른 상대적 가중치(dominant modality)를 비교(Ernst & Banks, 2002)해 볼 필요가 있다고도 생각 하였다. 이는 위치지각 정확성을 결정하는 촉지각 체계 역시 무엇에 해당하는 무게지각과 유사한 맥락의 물리적 특질(관성 텐서)로 상대적 우세성이 설명될 수 있을 것이라 추정되었기 때문이다.
따라서, 본 연구에서는 촉지각의 ”어디(where)?”를 알 수 있느냐의 문제에서 중요하게 작용하는 심리물리적(psychophysical) 속성을 관찰하기 위한 목적으로 다음과 같은 연구가설을 설정하였다. 첫째, 자극 크기 효과의 측면에서 손에 든 물체에 제공된 위치 지각 정확성은 압력의 크기와 유의미한 관계가 있을 것이다. 둘째, 자극 분포 효과의 측면에서 손에 든 물체에 제공된 위치 지각 정확성은 압력 분포와 유의미한 관계가 있을 것이다. 셋째, 자극의 크기와 분포 두 변수의 상대적 우세성의 측면에서, 손에 든 물체에 주어진 위치 지각의 정확성을 결정하는 특질은 압력의 크기보다는 물체를 잡고 있는 손의 회전축을 중심으로 한 압력의 분포와 더 유의미한 관계가 있을 것이다. 이러한 가설을 바탕으로 관찰된 결과는 많은 사전 연구들이 촉지각(haptic)의 운동 감각(kinesthetic) 정보와 피부 감각(cutaneous) 정보가 깊은 연관성을 가지고 있음을 함의하지만(Stevens & Rubin, 1970; Weber, 1834, 1978) 이들을 연결하는 속성을 표면적으로 논의하지 못했던(Millar, 1976, 1994) 부분을 다루어 보았다는 측면에서 높은 가치가 있을 것으로 기대한다.
본 연구에 참여하는 연구대상자는 내·외과적 질환이 없는 건강한 성인(실험과제에 대한 경험이 없는 총 20명)을 대상으로 하였다. 모든 피험자는 과제 수행의 제한이 없으며, 실험참여에 관한 연구윤리위원회의 승인(SNUIRB No.1509/002-002, ethical standards of the 1964 Declaration of Helsinki report ID 20481572) 하에 서면 동의서를 작성 한 후 과제에 참여 하였다.
실험 과제: 본 연구에서 사용하는 지각 정확성 과제는 주로 쓰는 팔을 가능한 편안한 위상을 유지하며(관찰결과 대부분 70~110도 사이에서 유지되는 것으로 나타남) 물체를 손으로 잡고 있는 상태에서 그 물체에 자극(충격)이 가해졌을 때 그 자극이 가해진 위치가 어디인지 판단하는 것이다(Turvey, 1996). 연구대상자는 사전에 제시된 조건에 따라 과제를 시작하며, 실험 동안 시각과 청각 정보는 차단되었다(Figure 1).
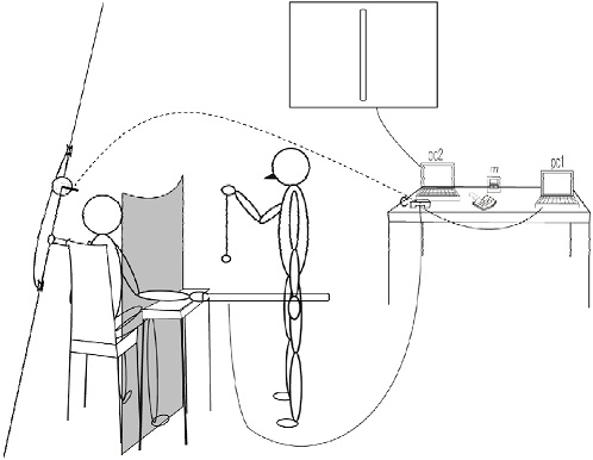
실험 절차: 실험에 앞서 연구대상자들에게 본 연구에서 수행해야 할 과제에 대한 설명과 사전 제작된 영상을 통한 시범을 제공하였다. 실험에서 과제 간(2수준) 다음 수행에 대한 시간적 제한을 두지 않았지만 과제 내(3수준) 이루어지는 시행에서는 제한(동일한 간격의 준비 시간)을 부여 하였으며 세부 과정은 다음과 같다.
실험 방법: 환경적 가변 요소(소음과 바람 등)가 차단된 실험실에서 연구대상자는 과제 수행 쪽 팔을 볼 수 없도록 한 차단막 옆에 헤드폰(청각자극차단)을 착용하고 앉는다. 실험용 도구는 나무막대(길이 40cm, 직경 1cm, 무게 180g)와 공(직경: 6.35-6.67cm, 무게: 56.7-58.5g, 압력: 254cm높이에서 콘크리트 바닥으로 떨어뜨렸을 때 135cm이상 147cm이하까지 튀어 오로는 정도)을 사용 하였다. 시각적으로 차단된 쪽에서 낙하 물체(공)를 연구대상자의 도구 위에 떨어뜨릴 때 연구대상자의 팔은 보조 받침대(i.e., rectangular desk) 위에 올려져 있고(동작을 최소화) 반대쪽에서는 접촉 지점의 위치를 나타내기 위해 연구대상자가 들고 있는 도구와 동일한 정향(degree), 길이와 척도(length = 40cm)로 제작된 위치 지정 장치가 있다. 떨어지는 공은 연구대상자가 들고 있는 막대로부터 조건 별 지정된 높이(30cm, 20cm, 10cm)와 거리(30cm, 20cm, 10cm)에서 동일한 속도와 구질로 떨어지도록 조건화 하였다(자료분석 모형 참고).
변환 프로그램(NI-Labview), 메트로놈(metronome) 등의 보조 장비와 연동된 진동 감지센서(T-Nest-vso300A1)를 활용하여 과제 내 다른 수준(30cm, 20cm, 10cm)에 따른 물리량(impulse)의 차이를 확인하였으며, 특히 동일한 수준으로 설정된 조건에서는 물리량이 연구대상자의 촉지각을 결정하는 요인이 되지 않도록 하였다[NI-Labview 시스템으로 측정한 서로 다른 높이 조건(3수준)에 해당하는 충격량: p=.856>.05]. 연구대상자는 낙하 물체가 도구에 접촉되는 것을 보거나 들을 수 없고 과제 및 거리별 무작위로 자신이 들고 있는 막대에 낙하 물체가 접촉되는 순간 도구를 들고 있지 않은 반대쪽에 설치된 위치지정 장치(Shwa & Turvey, 1992)를 이용하여 그 지점을 추정하였다.
자극의 강도 효과: 충돌하는 물체의 질량과 길이를 고정하고 동일한 질량 분포에서 수준(3)에 따른 자극 물체의 접촉 강도는 탄성(충돌) 계수[coefficient of restitution (e)]로써 조건화 하였다. 충격량과 운동량의 관계식에 의해 속도가 빠를수록 충격량은 커지는데, 이는 두 물체가 충돌하는 상황에서 탄성 계수로써 정리(Park & Kim, 2014)할 수 있다는 것을 바탕으로 하고 있다.
탄성 계수 (Coefficient of restitution): 충격량은 주이진 시간동안 가해진 힘의 합(Fdt)으로써 운동량(p = mv; m=질량, v=속도)의 변화(Δp = mv2 - mv1)가 바로 충격량(J)이다.
공식(2)은 시간에 대한 힘의 곡선을 적분( )한 것으로서, 충격량이 크면 운동량의 변화가 크다는 것을 의미하고 있다. 즉, 질량이 동일할 때 운동량은 속도의 변화로 반영되고, 속도가 빠를수록 충격량은 커지게 되는데, 이는 충돌하는 물체의 충돌 전·후 상대속도의 비율(v2 - u2 / v1 - u1)과 같은 물리량이 된다.
여기서 중요하게 다루어야 할 부분은 충돌 전과 후의 높이의 비율이 속도의 비율과 다르기에, 이를 속도의 비율로 나타내려면 충돌하는 물체가 자유 낙하할 때 이동한 거리와 속도의 관계를 고려해야 한다.
공식(4)에서, uf는 나중속도, ui는 처음속도, g는 중력가속도, h는 높이로써, 이를 물체의 충돌 전·후의 상대속도 비율에 적용하면 아래와 같이 전개될 수 있다.
위의 공식(5.1, 5.2)에 의하면 물체의 충돌 전 상대 속도( )는 0에서 자유 낙하한 물리량이고, 물체의 충돌 후 상대 속도( )는 0에서 리바운드한 높이가 된다. 따라서, 실제 상황에서는 충돌 전·후의 속도를 육안으로 식별하기가 어려우므로, 일정한 높이에서 물체를 자유낙하 시켜 튀어 오로는 높이( : NI-Labview 연동 위치 감지센서를 활용하여 측정 및 검증)를 통해 탄성계수(∴e)를 추정하고 이를 수량화 할 수 있다.
자극의 분포 효과: 충돌하는 물체의 질량과 길이를 고정하고 동일하게 표준화된 자극의 크기에서 수준(3)에 따른 자극의 분포는 접촉 지점의 조작을 통해 다르게 하였다. 이는 물체의 질량이 동일할 때 질량 중심이 중심축으로부터 멀리 위치할수록 적용된 저항과 운동 감각적 노력이 커진다는 원리를 이용한 것이다. 질량(m)을 상수(constant)로 할 때 물체를 손에 잡은 중심축으로부터 질량 중심의 거리(r), 즉 접촉 지점을 조작하면 압력의 분포(pressure distribution (l))와 충격 중심이 달라진다(Amazeen & Turvey, 1996)는 논리에 근거하고 있다.
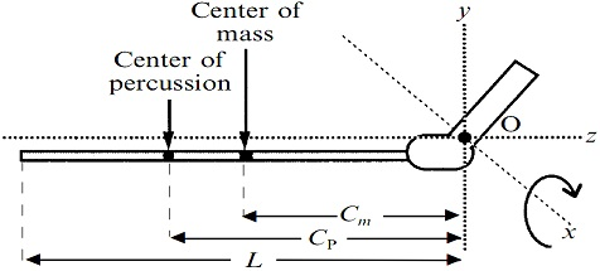
충격 중심(Center of Percussion): 도구(나무 막대)의 한 부분을 손으로 잡고 있을 때, 충격 중심은 도구를 잡고 있는 손의 중심축(origin at a center of rotation = O)을 기준으로 도구의 질량(m)이 x, y, z 축에서 상대적으로 어떻게 분포하고 있는지에 따라 특성화 될 수 있다.
위의 <Figure 2>처럼 단순한 형태에서 관성 능률은 물체의 질량과 손목(세가지 축의 토크가 0인 지점)으로부터 질량 중심까지의 거리에 의해 주어진다 (M = mCm). 이어서 물체의 움직임은 회전 가속으로 저항을 극복하도록 요구하는 구성인데 이는 질량분포의 두 번째 모멘트(Ixx = 1/3mL2)에 해당한다고 할 수 있다. 계산적 절차를 단순화하기 위해 도구의 직경을 상수로 간주하면 위와 같이 몇 가지 물리량(physical quantities)을 정의함으로써 손에 잡은 도구의 충격 중심을 추정할 수 있는데, 예를 들어 60cm 막대를 들고 있는 경우 (i.e., 손에 잡은 막대의 길이 63.5cm, 관성모먼트 302g · cm2) 충격 중심은 도구를 잡고 있는 손의 중심축으로부터 약 43.2cm 정도에 형성 될 수 있다.
자극의 강도와 분포의 크기 효과(확률 분석): 위의 두 정의(e = coefficient of restitution, I = pressure distribution)를 바탕으로 자극의 강도에 따른 촉지각의 정확성과 가변성, 자극의 분포에 따른 촉지각의 정확성과 가변성을 정량화하기 위해 상대 도수(Relative Frequency = Pj)를 적용하였다.
이는 변수(자극의 강도와 분포 정확성)의 변화 양상을 선형적으로 파악하기 위한 측면이며 추정된 결과(Pj, = cross sectional)의 통계적 검증은 Pearson’s Correlation(r = product-moment correlation coefficient)과 분산분석의 F-검증(ANOVA)을 통해 이루어졌다. 통계 분석의 유의 수준은 .05이다.
자극의 강도와 분포의 충돌 효과(시계열 분석): 자극의 상대적인 우세를 알아보기 위해 조건부 확률(Conditional Probability = P(A|B))
과 Stochastic 프로세스 마르코프 체인(Markov Chain)을 적용하였다.
이는 동일한 수준으로 변수를 조건화한 상태에서 시계열(t = level)에 따라 각기 다른 확률[Pj(n+1)]로 나타나는 상대적인 관계를 추정한 것이다.
탄성 계수(e)로 정의된 압력 자극의 크기에 따른 촉지각 위치 정확성은, 탄성 계수가 큰(H3=heigh level 3) 경우 추정의 오차가 가장 낮고(Absolute error size: M = 2.12, SD = 0.69), 중간(H2=height level 2)인 경우(Absolute error size: M = 2.73, SD = 0.55), 낮은(H1=height level 1) 경우 가장 높은(Absolute error size: M = 3.61, SD = 1.09) 것으로 나타나<Figure 3> 통계적으로 유의미한 차이를 보였다[F(2, 71) = 26.951 (p < 0.001), (Pearson Correlation R = - .61)].
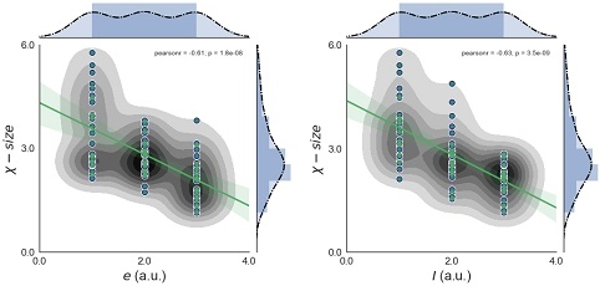
압력의 분포(I)로 정의된 중심축으로부터 접촉 거리에 따른 촉지각 위치 정확성은, 접촉위치가 먼(D3=distance level 3) 경우 추정의 오차가 가장 낮고(Absolute error size: M = 2.07, SD = 0.51), 중간(D2=distance level 2)인 경우(Absolute error size: M = 2.75, SD = 0.83), 가까운((D1=distance level 1) 경우 가장 높은(Absolute error size: M = 3.63, SD = .98) 것으로 나타나 통계적으로 유의미한 차이를 보였다[F(2, 71) = 28,865, (p < 0.001), (Pearson Correlation R = - .63)].
압력의 함수로써 어디(where)에 해당하는 촉지각의 위치 정확성은 동일한 분포의 압력에서 압력의 크기(충격량=탄성계수)와 비례하였을 뿐만 아니라, 동일한 크기의 압력에서 중심축으로부터 접촉 지점이 멀어질수록 지각 정확성이 높게 나타나 압력 (접촉거리=압력분포)의 분포와도 관계 하였다.
위의 확률 분포 결과를 바탕으로 자극의 수준(level=3)이 정확성의 정도를 결정하는 주요 요인임을 확인 할 수 있었다. 두 조건에 따른 상호작용 효과는 관찰되지 않았지만<Table 1, 2 (Two-way ANOVA, Crossed design) 참고> 추정된 주요 요인 간의 상대적인 우세를 알아보기 위해 조건부 확률 및 전이율[Pj(n+1)]을 계산하였다. 먼저, 탄성 계수가 증가함으로써 줄어드는 추정의 오차[Averaged absolute error size = 4.48 (Distance1: 1.89 = low 4.74 – high 2.85, Distance 2: 1.59 = low 3.58 – high 1.99, Distance 3: 1 = low 2.51 – high 1.51)]와 접촉 지점이 중심축에서 멀어짐으로써 생기는 추정의 오차[Averaged absolute error size = 4.64 (Height1: 2.23 = near 4.74 – far 2.51, Height 2: 1.07 = near 3.28 – far 2.21, Height 3: 1.34 = near 2.85 – far 1.51)]는 촉지각의 위치 지각 정확성에 유사한 크기로 기여 하였다.
각 조건별로 나누어 계산한 결과, 접촉 지점이 중심축에 가까운 조건에서 탄성 계수가 높은 경우(Absolute error size: blue line M = 2.85, SD = 0.52), 중간인 경우(Absolute error size: green line M = 3.28, SD = 0.42), 낮은 경우(Absolute error size: red line M = 4.74, SD = 0.67)로 추정의 오차가 나타났다. 접촉 지점이 중심축에 중간인 조건에서 충돌계수가 높은 경우(Absolute error size: blue line M = 1.99, SD = 0.37), 중간인 경우(Absolute error size: green line M = 2.69, SD = 0.26), 낮은 경우(Absolute error size: red line M = 3.58, SD = 0.77)로 추정의 오차가 나타났다. 접촉 지점이 중심축에서 먼 조건에서 탄성 계수가 높은 경우(Absolute error size: blue line M = 1.51, SD = 0.32), 중간인 경우(Absolute error size: green line M = 2.21, SD = 0.32), 낮은 경우(Absolute error size: red line M = 2.51, SD = 0.26)로 추정의 오차가 나타났다.
또한, <Figure 4>를 통해 알 수 있는 것과 같이 오차 추정의 평균과 가변성 모두 탄성 계수가 낮아지더라도 접촉 지점이 중심축에서 멀어지는 경우(Red line: H1+D3 = Absolute error size: blue line M = 2.85, SD = 0.52)가 탄성 계수가 높더라도 접촉지점이 중심축에서 가까워지는 경우(Blue line: H3+D1 = Absolute error size: red line M = 2.51, SD = 0.26)보다 상대적으로 더 적은 추정의 오차를 보였다. 동일한 크기로 조건화된 압력의 크기와 분포에서 위치지각 정화성의 추정과 변화율은 압력의 분포와 더 관계가 높은 것으로 나타났다.
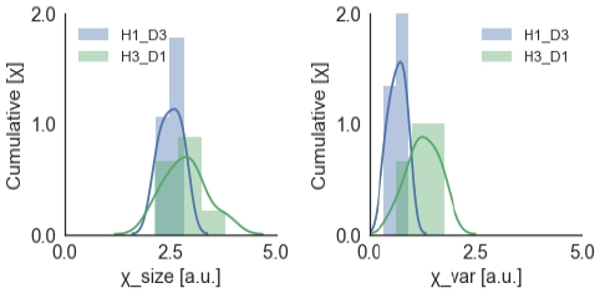
나아가서, 동일한 크기의 변화로 표준화된 두 조건에 따른 정확성 추정의 변화 정도(transitional probability)를 관찰한 결과(2-state) 접촉 지점이 중심축에서 멀어진 경우(H1+D3) 오차 추정 가변성의 전이율(transition rate)이 가장 크게 이루어지는 것으로 나타났다.
즉, 피부 압력을 통해 결정되는 위치지각 정확성은 압력의 크기만큼이나 압력의 분포에도 큰 영향을 받았고, 동일한 크기의 압력에서 중심축으로부터 접촉 지점이 멀어질수록 위치 지각 안정성이 상대적으로 더 좋아지는 것으로 나타났다.
본 연구는 지각 정확성과 관련한 사전 연구 결과들을 토대로 하고 있다. 특히, 무게지각에서 중요한 것으로 잘 알려진 속성이 주어진 자극의 위치(어디)를 지각하는 상황에서도 중요하게 작용하는지에 주요한 관심을 두었다. 이를 위해 연구대상자는 조건(2수준)별 지정된 높이(3수준)와 거리(3수준)에 따라 각각 다른 크기와 분포로 손에 잡은 도구에 전해지는 자극에 대한 위치 정확성을 추정하도록 요구되었다. 이는 (첫째) 손에든 물체에 자극이 가해진 위치를 보고하는 것이 진동을 통한 피부 압력 크기는 물론 (둘째) 압력 분포에도 영향을 받는지, (셋째) 같은 양으로 변화하도록 조건화 한 두 자극 양식 중 어느 양식에 더 큰 영향을 받는지 알아보고자 한 것이라 할 수 있다. 분석 결과 촉지각의 위치 정확성은 동일한 압력의 분포에서 압력의 크기와 비례하였다<Figure 3>. 그리고 동일한 크기의 압력에서 물체를 잡고 있는 중심축으로부터 접촉지점이 멀어질수록 지각 정확성이 높게 나타났다<Figure 4>. 즉, 위치지각 정확성은 자극의 크기(e)만큼이나 자극의 분포(I)와도 관계하였는데, 이러한 결과는 다음과 같은 특성에 의해 설명될 수 있을 것이다.
자극의 크기 효과: 일반적으로 손으로 들거나 휘두르는(hefting or wielding) 물체의 무게 지각(heaviness)은 중량의 함수(power function of weight) 관계로 증가한다.
하지만, 동일한 중량일지라도 무게 지각은 물체의 부피(volume)에 따라 다른데(log 함수 관계로 감소; Stevens & Rubin, 1970),
무게 지각을 결정하는 핵심적인 특질이 물체의 질량(m)은 물론 손에 잡은 물체의 저항과 관계된 회전 관성 (rotational inertia)과도 관계하기 때문이다(Amazeen & Turvey, 1996).
운동 감각을 통한 무게 지각이 물체의 질량(m = mass)뿐만 아니라 물체를 잡고 있는 회전축(O = location of rotation point)으로부터 위치한 질량(cm = location of the center of mass)의 분포와 관련된 회전 관성과도 관계하는 것처럼 동일한 압력에서 접촉 지점이 회전축으로부터 멀어질수록 더 큰 관성 텐서(inertia tensor)을 일으킨 본 연구의 결과는
자극을 통한 위치 지각 정확성이 압력의 크기뿐 아니라 압력의 분포에도 큰 영향을 받고 있다는 것으로 설명될 수 있는 결과라 할 수 있을 것이다.
자극의 충돌 효과: 본 연구의 실험적 검증에서 손에 잡은 도구의 위치 지각과 관련한 두 입력 양식(압력의 크기와 분포)을 동일한 양으로 조건화하여 비교한 결과 상대적으로 압력의 크기보다 압력의 분포에 더 안정적인 추정을 보이는 것으로 나타났다<Figure 4, Table 3>. 회전축으로부터 멀어질수록 위치 지각 정확성이 증가한다는 시·공간적 정보의 상대적인 기여는 어떤 체계에 근거한 과정일 수 있는지 아래와 같은 논리로 설명될 수 있을 것이다.
| Condition | Error_size | Error_variance | ||
|---|---|---|---|---|
| Height | Distance | Height | Distance | |
| 1 (10cm) | .22 | .22 | .21 | .21 |
| 2 (20cm) | .16 | .17 | .13 | .23 |
| 3 (30cm) | .13 | .11 | .16 | .07 |
먼저, 지각 정확성과 관련된 두 입력 정보 간의 우세성은 표준화(W) 된 변인[i = 자극 강도(e), 또는 자극 분포(I)]의 상대적인 크기에 따라 다르게 나타나는 최적 추정의 물리적 속성(S)으로 수치화 할 수 있다.
유기체의 신경계는 서로 다른 양상의 지각 체계들이 동시에 정보를 받아들여 일치되지 않을 경우 상대적 가중치에 따라 변이가 가장 낮게 추정된 지각 양상(modality)쪽으로 추정의 평균을 최적화하는 경향이 있다(Ernst & Banks, 2002). 관련된 대표적인 예로 동일한 질량의 물체이지만 부피(volume)나 크기(size)가 큰 것을 작은 것보다 더 무겁게 지각(Visual Size-Weight Illusion)한다. 그러나 동일한 질량이지만 직경(diameter)이 다른 두 물체를 보지 않고 손으로 다룰 경우 작은 직경(40mm)을 큰 직경(100mm)보다 오히려 더 무겁게 지각(Haptic Size-Weight Illusion: SWI)한다(Charpentier, 1891). 왜냐하면, 앞에서 논의한 바와 같이 무게 지각의 중요한 특질이 수행자의 내적 정보 통합(Information integration models by Anderson, 1970, 1972), 사전 경험을 통한 중추 기대(Motor command-expectation models by Davis & Brickett, 1977)뿐 아니라 상대적인 크기에 따라 다르게 나타나는 물리적 속성으로서 물체의 밀도 (Density models by Stevens & Rubin, 1970)와도 중요하게 관계하고 있기 때문이다.
손에 잡은 물체의 위치 지각 정확성이라는 본 연구 결과 역시 운동 감각과 밀접하게 관계된 것으로, 위치 지각을 결정하는 압력과 압력 분포 간 양적인 자극 특질이 관성 텐서(inertia tensor)로 잘 알려진 물리적 특질(Amazeen & Turvey, 1996)에 추정의 평균을 더 최적화 한 것으로 볼 수 있다. 지각된 무게(heaviness)가 물체의 질량(mass)과 크기(size)에 관계한다는 Weber (1834, 1978)의 통찰에서부터 기인한 촉지각(i.e., heaviness) 현상은 물체를 잡은 회전 지점(point of rotation)으로부터 질량이 어떻게 분포되어 있는지(mass distribution)에 의해 결정되는 물리적 특질(inertia tensor)로 설명되었다(Turvey, 1996; Carellro et al., 1999; Shockley et al., 2004; Streit et al., 2007; Harrison et al., 2011). 본 연구 결과에서 손에 잡은 물체의 지각된 위치(perceived point)를 결정하는 특질도 회전축을 중심으로 압력이 어떻게 분포하고 있는지에 영향을 받고 있었기 때문에 유사한 물리적 속성(intertia tensor)으로 설명될 수 있다는 견해이다.
다음으로, 이러한 회전 지점의 변화에 대한 압력 분포의 영향력은 손에 잡은 도구에 형성되는 충격 중심과도 관계가 있을 것으로 보인다. Carello et al., (1999)에 의하면 회전 지점의 변화에 대한 질량 분포의 형성(moment of inertia)은 손에 잡은 물체의 충돌과 관련하여 가장 이상적인 타격점(sweet spot)으로 나타나는 충격 중심(center of percussion)의 형성과 깊은 관계가 있다(Solomon & Turvey, 1988; Carello et al., 1999). 본 실험에서 나타난 동일한 크기의 압력에서 접촉 지점이 멀어질수록 가변성이 줄어들고, 접촉 지점 3(Distance 3 = 30cm)이면서 접촉 물체가 떨어지는 높이가 1(height 1 = 10cm)인 경우가 접촉 지점이 1(Distance 1 = 10cm)이면서 접촉 물체가 떨어지는 높이가 3(height 3 = 30cm)인 경우보다 지각 정확성이 높게 나타났다. 이는 촉지각 위치 추정의 오차(absolute error size)와 가변성(variability)이 충격 중심에 가까울수록 줄어든다는 것을 의미한다고 볼 수 있는 결과라고 생각 한다. 이 근접성이 충돌을 통한 추정의 오차와 가변성에 영향을 준 것으로 짐작할 수 있겠다. 이는 곧, 간단한 물리량의 계산으로 추정되는 충격 중심의 위치 정확성(where)과 더불어 수행자에게 무슨(what) 일이 일어나는지와 관련된 중요한 통찰(Lederman & Klatzky, 2009)을 제공할 수 있는 결과라고 생각한다.
결론 및 제언: 본 연구는 손에 든 물체의 지각에 대한 운동 감각적 접근을 바탕으로 하고 있다. 촉지각 정확성 기전(mechanisms)과 관련한 조금 더 구체적인 차원에서 위치 지각 현상을 들여다보고자 하였다. 기존 연구의 움직임과 운동을 통한 물리적 기능 유지라는 일차원적인 상관관계를 지향하기보다 심리·물리적 설계를 통하여 확장될 수 있는 지각적 변화에 대한 주제에 초점을 맞추었다. 이는 촉지각 작용에 대한 다차원적인 접근을 가능하게 할 수 있을 것이며 실험의 설계 및 분석을 통해 나타난 결과들은 촉지각 현상에 대한 사전연구 결과들을 더욱 확장시킬 수 있을 것으로 사료된다. 특히 도구를 사용하는 상황, 즉 비시각적 촉지각 능력의 영향을 많이 받는 종목에서 운동 기구의 제작 및 수행자의 기술 수준을 비교하기 위한 지표이자 더 정밀한 측면에서 효율성을 확보하는 방법으로 기여할 수 있을 것으로 기대한다.
Harrison, S. J., Hajnal, A., Lopresti-Goodman, S., Isenhower, R. W., & Kinsella-Shaw, J. M. (2011). Perceiving action-relevant properties of tools through dynamic touch: Effects of mass distribution, exploration style, and intention. Journal of Experimental Psychology: Human Perception and Performance, 37(1), 193.