 ISSN : 1598-2920
ISSN : 1598-2920
© Korea Institute of Sport Science
The purpose of this study was to explore the optimal model for winning medal on vault event of men's gymnastics. Specifically, decision tree analysis was used to explore, first, for the optimal conditions for qualifying top 8th player that have high possibility into final round, and second, for the optimal model for obtaining the medal of the vault event.
Data were collected for five official competitions (Olympics, Asian games, and International championship, etc.) organized by the Federation of International Gymnastics (FIG) from 2013 to 2016. In this study, the data of 626 vault players were collected. Also all of these players performed 921 vault skills for qualifying round or final round. Five predictor variables for estimating for qualifying into the final round and for obtaining the medal of the vault event were selected; nationality, difficulty score, acting score, additional penalty score, final score.
The results is as follows. Overall, it was confirmed that the optimal model for entering into the final round was the difficulty score of vault event. The optimal model for entering into the final round estimates 81.2% when condition would be the 5.6 or higher of difficulty score and 8.6 or higher of the acting score. The optimal model for winning medals was 86.7%, which means that when condition would be the 6.0 or higher of difficulty score and no additional penalty score.
이 연구는 남자체조 도마 종목의 메달획득 예측을 위한 최적의 모형을 탐색하는 것이 목적이다. 구체적으로 첫째, 도마의 선수들이 단체전 도마경기와 종목별 개인 도마경기에서 상위 8위 점수를 획득할 수 있는 최적의 조건을 탐색하고, 둘째, 결승라운드에 진출한 도마 선수들의 메달획득을 위한 조건을 분석하는 것이다.
2013년부터 2016까지 수행된 국제체조연맹 주관의 세계대회(올림픽, 아시안게임, 세계선수권대회 등)를 대상으로 하여 도마 종목에 출전한 626명의 선수 자료를 수집하였다. 이들 선수들이 수행한 961개의 도마 기술을 구분하였다. 도마 종목에 출전한 선수들이 수행한 961개의 기술을 분류하여 선수의 국적, 해당기술의 난도점수, 실행점수, 추가감점, 최종점수 등을 기록하였다. 의사결정나무 분석의 CHAID 방법을 적용하여 분류정확확률, 이익도표 등을 산출하였다.
전체적으로 체조 도마경기의 경기력을 설명하는데 있어, 가장 크게 영향을 미치는 것은 기술의 난도점수로 나타났다. 국제 체조경기 도마 종목에 출전한 선수들이 예선라운드에서 난도점수가 5.6 이상 그리고 실행점수가 8.6 이상 획득하였다면 81.2%로 결승진출 가능성 높은 선수로 예측할 수 있다. 또한 결승라운드에 진출한 도마 종목 선수들이 6.0 이상의 난도점수의 기술 수행으로 추가감점이 없다면 메달획득 가능성은 86.7%로 나타났다.
한국 기계체조는 올림픽, 아시안게임 등의 메가-이벤트 대회에서 다수의 메달을 획득하며 대한민국의 스포츠 위상을 높이는데 기여해 왔다. 남자6종목(마루, 안마, 링, 도마, 평행봉, 철봉), 여자4종목(도마, 이단평행봉, 평균대, 마루)으로 구성된 기계체조 세부 종목 중에서 도마 종목은 한국 체조를 세계 정상급으로 올리는데 중요한 역할을 담당해 왔다(Kim, 2017; Yoon, Yang, Park, & Yoon, 2018). 특히 남자 도마경기는 우리나라가 올림픽 금메달을 획득한 종목일 뿐 아니라 여1, 여2, 양1, 양2 등과 같은 국내 선수들이 만들어 낸 신기술을 세계연맹의 기술로 등재하여 한국 기계체조 종목의 위상을 구축해왔다.
도마 종목은 도움닫기, 구름판을 밟아 양손으로 도마를 짚는 1비약, 도마를 짚은 후 공중기술을 수행하는 2비약, 착지로 구성되며 이중에서 1비약, 2비약, 착지에 대하여 평가를 받는다(Park, & Song, 2015). 도마종목에서 선수들은 단일기술 수행(연기)에 대한 평가를 받기 때문에 기계체조 종목 중 가장 짧은 시간에 연기를 수행해야 하는 특성을 갖는다. 따라서 가급적 선수들은 높은 난이도의 기술을 선택(Park, & Song, 2012; FIG, 2017)하여 성공하는 것이 도마경기 메달 획득을 위한 주요변수로 작용한다. 신기술 개발 역시 메달획득을 위해 중요한 요소 중 하나이다. 신기술을 개발한 후, 국제대회에서 신기술을 성공한다면 세계체조연맹(Federation of International Gymnastics: FIG)은 해당 기술에 대하여 최고 난도 점수를 부여하기 때문이다. 도마종목 선수들이 메달 획득을 위해 부상위험을 감수하고서라도 고난이도의 기술 수행에 초점을 맞추는 이유이다(Yoon et al., 2018; Han & Jung, 2012).
한편, FIG는 기계체조 기술발전을 도모하기 위하여 올림픽 주기인 4년에 맞추어 종목별 기술 규정을 개정한다. FIG가 개정하는 기술규정은 기술별 난도 점수, 특별요구조건, 감점요소 등을 포함하고 있다. 또한 신기술이 개발될 때 마다 기술의 난도 점수를 수시로 추가한다(FIG, 2017). 이는 선수들에게 끊임없이 새로운 규정에 적응도록 하며 동시에 신기술 개발을 촉진시키는 작용을 한다. 따라서 현장지도자 및 선수들은 변화하는 규칙에 적응하기 위해 훈련하고, 신기술 습득을 위하여 노력하고 있다(Han et al., 2012).
도마 종목의 기술 향상을 위한 학계의 노력도 적지 않다. Yoon et al.(2018)은 도마 종목의 기술 향상을 위하여 기술수행의 기본이 되는 도움닫기 및 발 구름 동작을 운동역학적으로 분석한 바 있으며, Song & Park(2016)은 북한 리세광선수의 도마 기술에 대한 운동학적 특성을 연구하여 우리나라 도마선수들의 기술향상 방안을 위한 기초자료를 제공한바 있다. 또한 Kim(2018)과 Han et al.͏(2012)은 세계선수권 남자도마 결승경기 내용분석을 통하여 도마 결승경기의 경기력 결정요인을 분석한바 있다.
기존의 선행연구는 도마 경기의 내용분석과 동작 분석을 통하여 도마기술의 성공패턴, 도움닫기 기술의 중요성 등에 대한 실증적 자료를 제시함으로써 도마 종목의 효과적인 경기 수행을 위한 유익한 정보를 제공하였고, 도마 종목에서의 메달획득을 위한 전략 수립의 기초자료를 제공해 온 것이 사실이다. 특히, 선행연구는 국내 도마 종목 선수들의 특성을 바탕으로 효과적인 동작모델을 제시하였다는 점에서 현장에서의 가치도 적지 않다. 그럼에도 불구하고 선행연구는 개별 기술에 대한 분석에 대하여 주된 관심을 두어왔기 때문에 다양한 변수가 존재하는 실제 경기 현장에서 어떤 요소를 우선적으로 고려하여 선수들이 경기를 준비해야하는지에 대한 정보는 제한적으로 제공할 수밖에 없었다.
예컨대, 도마 경기에서 선수들이 메달 획득 여부는 도마 경기의 기술들이 가지고 있는 운동학적특성 뿐 아니라 난도 점수, 실행 점수, 추가감점 등 다양한 변수들이 영향을 미치게 된다. 어떤 변수들이 메달획득에 주로 영향을 끼치는지, 또는 어떤 변수들이 상대적으로 메달획득에 영향이 적은지는 현장 지도자들에게 매우 의미 있는 정보가 될 것이다. 이 문제는 의사결정나무(decision tree) 분석을 통해 해결 가능하다.
의사결정나무분석은 어떤 사건을 예측하거나 분류하기 위한 방법으로 데이터 마이닝 분야에서 활용되어 왔다. 의사결정나무분석은 의사결정의 규칙을 나무구조로 도표화하여 관심 대상이 되는 종속변수의 특성을 예측하거나 분류한다(Kim, Park, & Kang, 2006). 즉 의사결정나무 분석에서는 자료를 탐색하고, 불필요한 자료에 대하여 가지치기를 수행한 후, 남은 자료를 대상으로 하여 모델링 한다. 다시 말해 도마경기의 다양한 변수들 중 메달획득을 예측하는데 있어 불필요한 변수는 가지치기 하여 버리고, 필요한 변수만을 대상으로 메달획득 예측을 위한 모델링이 가능하다는 것이다. 방대한 정보를 활용해 정보를 축약하는데 탁월한 장점을 갖고 있다. 반면, 의사결정나무분석은 투입한 변수의 범위 내에서 모델링해야한다는 한계와 함께, 시계열적 분석이 불가능하고 분석용 자료에 의존하여 모델링하기 때문에 새로운 자료를 적용하여 예측할 때 안정성이 떨어질 수 있다는 단점도 존재(Alamar, 2013)한다.
그럼에도 불구하고 이 연구는 의사결정나무 분석은 나무구조에 의한 추론규칙을 따르기 때문에 데이터마이닝을 목적으로 수행하는 다른 분석방법들과 비교할 때 결과해석이 용이하고 변수 간 상호작용효과를 쉽게 확인할 수 있다. 특히 질적변수 및 양적변수에 대한 자료분석이 가능하고, 모수통계의 기본가정(선형성, 정규분포성, 등분산성)을 따르지 않아도 분석이 가능하기 때문에 현장에서 쉽게 활용할 수 있다(Kim, Lee, & Lee, 2012; Choi, & Yoon, 2017; Berry & Linoff, 2000). 이와 같은 이유 때문에 의사결정나무분석은 스포츠 상황을 분류 및 예측하기 위해 다양한 종목에서 적용되어 왔으며, 이 연구는 도마 종목의 메달 획득을 위한 최적의 조건을 추출하는 목적으로 의사결정나무분석이 적합한 것으로 판단하였다.
따라서 이 연구에서는 남자 기계체조 도마경기 메달 획득을 위한 최적모형을 탐색하는 것을 목적으로 설계하였다. 도마 종목은 예선경기와, 결승경기로 구분된다. 도마 예선경기의 결과에 따라 최종 8명만이 결승경기에 진출하여 경기를 치른 후 성적에 따라 금, 은, 동메달을 가린다. 이 연구의 연구문제는 다음과 같다. 첫째, ‘도마 예선경기에서 결승에 진출할 가능성이 높은 단체전 도마경기 및 개인 종목별 도마경기의 8위 이내 성적 획득을 위한 최적의 조건은 무엇인가?’와 둘째, ‘도마 결승경기에서 메달을 획득하기 위한 최적의 조건은 무엇인가?’이다. 의사결정나무분석을 활용하여 세계대회에 출전한 선수들의 결승진출 가능성이 높은 선수들의 특성과 결승에 진출하였을 때 메달획득 조건을 탐색하여 도마 경기력 향상을 위한 기초자료를 제공하고자 한다.
이 연구는 남자 기계체조 도마 종목에 출전한 선수들의 메달 획득을 위한 최적모형을 탐색하는 것이 목적이다. 이 목적을 위하여 2013년부터 2016년까지의 FIG 공식대회 중 2014년 인천아시아경기대회, 2013년 벨기에세계선수권대회, 2014년 중국세계선수권대회, 2015년 영국세계선수권대회 및 2016년 리우올림픽대회의 자료를 대상으로 수집하였다. 자료는 세계체조연맹에서 제공하는 공식 대회 기록과 함께 유튜브에서 제공하는 대회의 영상자료를 통해 체조 도마 선수들이 수행한 기술을 기록하였다. 이 연구의 범위로 설정한 4년의 기간 동안 5개 세계대회에서 도마 종목에 참가한 선수는 전체 626명이며, 626명이 수행하였던 기술의 횟수는 전체 961개이었다. 구체적인 연구대상 자료의 특성은 <Table 1>과 같다.
| Year | Competition | Number of players | Number of performance |
|---|---|---|---|
| 2013 | 44th World Championships (Belgium) | 42 | 100 |
| 2014 | 17th Incheon Asian Games | 61 | 128 |
| 2014 | 45th World Championships (China) | 249 | 329 |
| 2015 | 46th World Championships (England) | 228 | 308 |
| 2016 | 31st Rio Olympic | 46 | 96 |
| Total | 626 | 961 | |
도마경기에 수행되었던 961개의 기술을 결승진출 가능성이 높은 선수와 메달획득 선수에 따라서 재분류하였다. 먼저 다섯 개의 대회에 출전한 626명의 선수들 중 도마종목에 결승진출 가능성이 높은 선수의 특성을 분석하고자 하였다. 도마 종목 결승진출 가능성이 높은 선수는 8위 이내에 성적이 랭크되어야함으로 단체전 도마경기에서 8위 이내의 선수와 개인전 도마경기의 각각의 시도(1차시도와 2차시도)별 8위 이내의 선수로 정의하였다. 이 기준에 의해서 결승진출 가능성이 높은 8위 이내 선수들은 138명이었고, 다섯 개 대회에서 금, 은, 동메달을 획득한 선수는 모두 15명이었다. 이는 결승진출 가능성이 낮은 선수 그리고 메달을 획득하지 못한 일반선수와 지나치게 큰 사례수의 차이를 발생하게 된다. 이 연구는 무작위 표본추출 절차를 통해 626명의 선수들 중에서 결승진출 가능성 높은 선수 및 메달획득 선수와 동일한 138명과 15명의 선수를 재선정하여 분석에 활용하였다. 따라서 도마종목의 결승진출 가능성 추론 모형은 276명(상위 8명의 시행별 도마성적 우수 선수 138명과 일반선수 138명) 그리고 메달획득모형은 30명(메달획득 선수 15명과 메달 미획득 선수 15명)의 도마선수를 대상으로 모델링하였음을 밝혀둔다. <Table 1>은 각 대회별 출전선수와 선수들의 기술시행 횟수를 제시한 것이다. 앞에 제시한 도마 종목 결승진출 가능성 높은 선수의 정의에 따라 개인전 도마경기 시행(2회)과 단체전 도마경기 시행(1회 또는 2회)이 포함되어 있다.
세계체조연맹(FIG)에서는 FIG에서 주관하는 경기에 대하여 각 종목별, 선수별 기술에 대한 난도점수, 실행점수, 추가감점, 최종점수, 순위 등에 경기결과와 함께 출전선수에 대한 정보(성별, 국가 등)를 제공하고 있다. 이 연구는 도마경기 메달획득을 위한 최적조건을 탐색하는 것이 목적이다. 이 목적을 위하여 목표변수로 결승진출 가능성 높은 선수의 특성과 메달획득 가능성을 선정하였으며, 분류변수로 도마출전선수에 대한 인구통계학적 정보(국가) 및 경기결과에 해당하는 5개의 변수를 분류변수로 선정하였다.
의사결정나무분석은 연속형 변수를 투입하더라도 통계적 모델링의 유의도를 근거로 비연속형으로 결과를 산출하기 때문에 예측의 오류 또는 예측력의 감소를 유발(Jang, Hong, & Jang, 1999)할 수 있음을 유의해야 한다. 특히, 전적으로 통계적 결과만을 바탕으로 한 연속형 변수의 불연속형으로 변형시키는 것은 연구에서 변수가 갖는 의미를 다르게 해석될 수도 있다. 이에 따라 이 연구는 모든 투입변수를 범주형으로 변환하였다. 이때 중위수를 선택하여 범주형 변환이 이루어졌다. 또한 이 연구의 대상으로 삼은 다섯 개의 대회에 출전한 도마선수는 60여 개국 이상의 다양한 국적을 가지고 있다. 이 연구는 아시안 선수들이 체조도마경기에서 질적 평가의 편파성 여부에 관심을 갖고 아시안 선수와 비아시안 선수로 이분화 하여 구분하였다. 따라서 이 연구는 아프리카, 유럽 등 대륙별 특성에 관심을 두지 않고 단지 아시아권 선수여부만을 관심에 두어, 아시안과 비아시안 선수로 국적변수를 투입하였다. 이 연구의 투입변수에 대한 정의는 <Table 2>에 제시하였다.
| Variable | Description of Variable |
|---|---|
| Classification variable | |
| Nationality | The nationality of a player is divided into Asian and non-Asian. |
| Difficulty score: D-scored | Categorization of the difficulty score of the skill performed by the athlete based on the median. |
| Execution score: E-score | Categorization of the execution score of the skill performed by the athlete based
on the median. Execution score = Total score 10point - deduction about technical performance |
| Additional deduction | Deducted when a player touching the mat with any part of the body outside of the marked corridor (landing line). |
| Total score | Total score = D-score + E-score+ Additional deduction |
| Ranking | Ranking of the players according to their final score |
| Target variable | |
| Possibility to final entry | Qualifying top 8th player that have high possibility into final round |
| Medal acquisition | Players who from the 1st to 3rd in finals |
이 연구에서 의사결정나무 분석을 위한 알고리즘은 CHAID(chi-squared automatic interaction decision)방법을 선택하였다. 의사결경 분석 알고리즘은 CHAID를 포함하여 CART(classification and regression trees), QUEST(quick, unbiased, efficient, statistical tree) 등이 소개되고 있는데, 이 연구에서는 범주형, 연속형 등 모든 종류의 목표변수와 분류변수에 적용이 용이하며, 목표변수가 범주형인 경우 각 범주에 속하는 빈도에 따라 자식마디를 분리할 수 있는 CHAID 방법을 선택하였다.
이 연구에서는 CHAID 알고리즘을 적용하여 분석 수행하였으며 이때 사용한 분리기준은 카이제곱 통계량과 유의도 값을 활용하였다. 카이제곱 통계량의 계산은 다음 <Equation 1>과 같다.
Here,
eij = The expected frequency for the jth result of the ith group
fij = The observed frequency for the ith result of the jth group
이 연구에서 적용한 의사결정나무분석은 3단계까지 자식마디의 깊이를 설정하였으며, 부모마디의 최소사례는 연구팀 협의를 통해 최소사례의 1/3에 해당하는 10, 자식마디의 최소사례는 5로 설정하였다. 즉, 5 이하의 자식마디 사례가 나타난다면 분류를 종료한다는 것을 의미한다. 의사결정나무분석의 예측모형의 적절성에 대한 평가는 정오분류표를 활용하였다. 정오분류표 평가방법은 목표변수가 범주형일 때 적용할 수 있는 방법이다(Kim et al, 2006). 정분류율과 오분류율의 계산은 <Equation 2>, <Equation 3>과 같다. CHAID 방법에서 노드분할(Splitting)과 범주병합(Merging)에 대한 유의수준은 모두 .05로 설정하였으며, 모든 통계적 처리는 IBM SPSS 25.0을 활용하였다.
이 연구에서는 남자 기계체조 도마경기 메달 획득을 위한 최적모형을 탐색하는 것이 목적이다. 구체적으로는 의사결정나무분석을 활용하여 도마경기 결승진출 가능성 높은 선수의 특성파악을 위한 최적모형과 도마결승경기 메달획득을 위한 최적모형을 탐색하여 도마경기 경기력 향상을 위한 기초자료를 제공하고자 하였다.
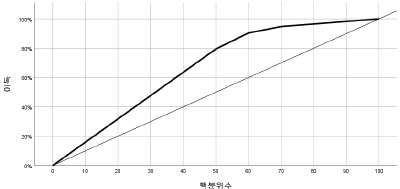
남자 기계체조 도마경기 결승진출 가능성이 높은 선수의 특성을 탐색하기 위하여 국적, 난도점수, 실행점수, 추가감점, 최종점수를 분류변수로 지정하여 분석을 실시하였다. 분석결과 분류변수로 포함된 변수는 난도점수, 실행점수, 국적이며, 구체적인 결과는 <Fig. 1>과 <Table 3>에 제시하였다.
| Nodes | Node | Gain | Response | Index |
 |
||
|---|---|---|---|---|---|---|---|
| n | % | n | % | % | % | ||
| 3 | 146 | 52.9 | 116 | 81.4 | 79.5 | 158.9 | |
| 4 | 17 | 6.2 | 8 | 5.8 | 47.1 | 94.1 | |
| 6 | 21 | 7.6 | 6 | 4.3 | 28.6 | 57.1 | |
이 연구에서 목표변수인 결승진출 가능성이 높은 선수 특성은 도마예선경기에 출전하였던 선수 중 예선통과 기준인 8위안에 속했음을 의미한다. 의사결정나무 분석의 구조에서는 가장 영향력 있는 예측변수가 상위에 위치하게 되고 영향력의 정도에 따라 예측변수가 계층적으로 위치한다(Kim, Park, Park, & Cho, 2013). 즉 최적모형의 첫 번째 분류기준은 결승진출 가능성 높은 선수특성을 예측하는데 가장 높은 설명력을 갖는다는 것을 의미한다. 이와 같은 관점에서 해석할 때 결승진출 가능성 높은 선수특성의 첫 번째 분류기준은 난도점수(χ 2=107, p=.001)인 것으로 나타났다. 난도점수가 5.6이상인 경우 결승에 진출할 확률이 76.1%로 나타났으며, 반대로 5.6이하인 경우 결승진출 가능성 높은 선수에 포함되지 않을 확률이 87.6%인 것으로 나타났다. 또한 난도점수가 5.6이상 일 때 실행점수가 8.6이상인 경우 결승에 진출 할 확률이 79.5%이며 8.6이하인 경우 결승에 진출 할 확률이 47.1%로 나타났다(χ 2=8.684, p=.003).
반면, 난도점수가 5.6이하 일 때 국적 여부가 결승진출 가능성 높은 선수로 분류될 가능성에 미치는 것으로 나타났다. 즉 난도점수가 5.6이하이면서 국적이 아시안 일 경우 결승에 진출할 확률은 28.6%로 나타났지만 비아시안일 경우 8.7%가 결승에 진출할 가능성을 나타내는 것으로 확인되었다(χ 2=6.037, p=.014). 더불어 비아시안일 경우 실행점수가 결승진출 가능성 높은 선수의 특성에 영향을 미치는 것으로 나타났다. 즉 비아시안 이면서 실행점수가 8.6이상인 경우 결승진출 가능성 높은 선수로 분류될 확률이 10.7%로 나타난 반면 실행점수가 8.6이하인 경우 결승에 진출할 확률이 0.0%인 것으로 나타났다(χ 2=͏20.806, p=.001).
<Table 3>에 요약된 노드는 도마 종목 결승진출 가능성 높은 선수특성 파악을 위한 최적모형의 이익도표와 ROC를 나타낸 것이다. 남자체조 도마 종목의 결승진출 가능성 높은 선수특성 분석을 위한 최적모형은 146명의 선수가 해당되는 3번 노드인 것으로 나타났다. 3번 노드는 난도점수 5.6이상의 선수들 중에서 실행점수 8.6 이상인 선수들이 이에 해당한다. 도마선수의 결승진출 가능성 높은 선수로 예측하는데 81.4%의 이득이 기대할 수 있으며, 이 조건에 해당하는 도마 선수의 결승진출 가능성 높은 선수로 분류될 가능성이 158.9% 증가하는 것으로 나타났다. 남자 도마 종목의 결승진출 가능성 높은 선수 특성파악을 위한 차선의 모형은 17명의 선수들이 해당되는 4번 노드였다. 4번 노드는 난도점수 5.6 이상 수행한 선수들 중 8.6 미만의 실행점수를 획득한 선수들이다. 결승진출 가능성 높은 선수로 예측이득은 5.8%로 낮기 때문에 큰 의미는 부여하지 않는다.
FIG가 주관하는 공식 세계대회는 예선경기를 치른 후, 점수 순서대로 8명의 선수들이 결승 라운드에 진출하여 최종 1위, 2위, 3위를 가린다. 이 연구는 2013-2016 규칙을 적용하는 동안 FIG가 주관하는 공식 세계대회인 1회의 아시아경기, 1회의 올림픽대회, 3회의 세계선수권대회를 포함하였다. 다섯 개 대회를 대상으로 하였기 때문에 금메달, 은메달, 동메달 획득을 위한 최적 모형을 위해서 산정되는 메달의 개수는 15개(5개 대회 × 메달 수)이다. 따라서 15개의 사례에 해당하는 15명의 메달획득 실패 사례를 무작위로 선정하였다. 따라서 한정된 사례 수에 따른 결과해석에 주의가 요구된다는 사실을 밝혀둔다.
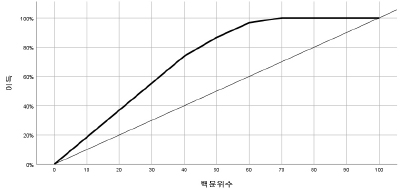
남자 기계체조 도마경기 메달획득을 위한 최적모형을 탐색하기 위하여 국적, 난도점수, 실행점수, 추가감점, 최종점수를 분류변수로 투입하였으며 분석 결과 난도점수와 추가감점이 분류변수로 포함되었다. 구체적인 결과는 <Fig. 2>와 <Table 4>에 제시하였다.
| Nodes | node | Gain | Response | Index |
 |
||
|---|---|---|---|---|---|---|---|
| n | % | n | % | % | % | ||
| 3 | 13 | 43.3 | 12 | 80.0 | 92.3 | 184.6 | |
| 4 | 6 | 20.0 | 3 | 20.0 | 50.5 | 100 | |
| 2 | 11 | 36.7 | 0 | 0.0 | 0.0 | 0.0 | |
그림에서 확인하듯 도마경기에서 메달획득을 위한 첫 번째 분류기준 변수는 선수들의 난도점수(χ2=17.368, p=.001)인 것으로 나타났다. 결승에 진출한 도마 종목의 선수가 6점 이상의 난도점수로 경기를 수행하였을 경우 메달획득 가능성이 78.9%로 나타났다. 특히 도마 종목 결승진출 선수들이 6점 이하의 난도로 경기를 수행하였다면 메달획득에 실패한 사례가 100%였다. 도마 선수들이 수행하는 난도 점수는 결승진출 가능성 높은 선수의 특성 및 메달획득 가능성을 점칠 수 있는 가장 중요한 예측변수로 나타났다. 또한 6점 이상의 난도점수로 경기를 수행한 도마 선수라면 메달획득 가능성은 추가감점여부에 따라서 달라지는 것으로 나타났다. 즉 난도점수가 6점 이상이면서 추가감점이 없을 경우 메달을 획득할 확률은 92.3%이다(χ2͏=4.421, p=.035).
<Table 4>에 요약된 도마 종목 메달획득을 위한 최적모형은 도마 종목 결승 라운드에서 난도점수 6이상을 수행한 선수들이 추가감점이 없는 조건인 3번 노드로 나타났다. 3번 노드의 조건에 해당된다면 결승 라운드에서 메달획득 가능성이 184% 증가한다.
우리나라 기계체조의 도마 종목은 올림픽 대회에서 금메달 한 개, 은메달 한 개, 동메달 두 개를 획득한 효자 종목이다. 이에 체육학분야 연구자들은 기계체조 도마경기의 메달획득을 위한 다양한 노력(운동역학적 분석, 내용분석)들을 시도하여 왔으며(Kim, 2017; Yoon et al., 2018; Han et al., 2012), 그 노력의 결과들은 실제 경기력향상에 기여해 온 것으로 평가할 수 있다.
이 연구는 기계체조 도마경기에서 메달획득을 위한 최적의 조건을 탐색하기 위한 목적에서 시작하였다. 도마경기에서 메달획득은 다양한 조건에 의하여 영향을 받음에도 불구하고 전통적으로 개인의 동작분석과 같은 단일 변수에 초점이 맞추어져 왔다. 경기내용분석을 통해 전체적인 관점에서 메달획득 요인을 찾고자 하는 시도들이 주를 이루고 있던 것이 사실이다. 뿐만 아니라 도마경기의 메달획득을 위한 예선전 경기에 대한 중요성이 적지 않음에도 불구하고 예선전 경기 내용에 대한 분석이 부재했던 것 도 사실이다. 따라서 이 연구는 예선전을 통과하기 위한 조건 그리고 결승전 경기에서 메달획득을 위한 조건에 대한 최적모형을 탐색하고자 하였다.
이 연구의 결과 도마 경기에 출전한 선수들이 결승전에 진출하는 최적 분류변수는 난도점수인 것으로 확인되었다. 난도점수는 최소 5.6이상의 난도로 수행하고 실행점수는 8.6이상을 받는다는 조건이 결승진출 가능성 높은 선수의 특성인 것으로 밝혀졌다. 흥미로운 사실은 선수들이 5.6이하의 난도의 연기를 수행한 경우 아시아권 선수들보다 비아시아권 선수들이 더 큰 패널티를 받는 다는 것이다. 난도점수 5.6이하에서 비아시아선수들의 뿌리마디로 실행점수가 도출되었다는 사실을 통하여 한 가지 추측 가능한 것은 아시아선수들이 비아시아선수들에 비하여 실행점수를 보다 높게 받기 때문으로 판단해 볼 수 있다. 그러나 그 이유가 국적이 갖는 이점(advantage) 때문인지 혹은 실제 기술의 완성도가 아시아인이 더 높기 때문인지에 대하여는 이 연구에서 확인할 수 없었다. 도마 종목의 기술 수행에 있어 인종에 따른 차이는 흥미로운 주제이며, 후속연구를 통하여 규명될 수 있길 기대해 본다.
결승 라운드에 진출한 도마 종목 선수들의 메달획득 가능성을 분별하는데 가장 큰 영향력을 미치는 변수는 난도점수였다. 특히 난도점수와 추가감점 여부만으로 92%의 도마 종목 선수들의 메달획득 여부를 예측해 낼 수 있다는 점에서 시사점이 적지 않다. 도마 종목에서 선수들이 획득하는 최종점수는 난도점수, 실행점수, 추가감점의 합으로 결정되는데, 결승 라운드에 진출한 세계정상급 선수들은 기술에 대한 완성도는 높기 때문에 실행점수에 의한 메달획득 가능성 여부는 변수가 되지 않는다고 판단할 수 있다. 즉, 도마 종목 선수들은 결승 라운드에서 기술수행에 있어 추가감점을 줄 일 수 있다면 메달획득이 가능성을 높일 수 있다는 논리가 성립된다. 빅이벤트급 대회의 도마경기 메달권 선수들의 실행점수가 9.0을 넘지 않는다(Han et al., 2012)는 연구결과도 이 주장을 지지하고 있다.
한편, 난도점수가 6점 이상일 경우 추가감점이 없을 경우 메달획득 확률이 높은 것으로 나타났다. 추가감점은 착지 시 착지범위를 벗어나는 정도에 따라 주어지는 감점이다(FIG, 2017). 대부분 기술수행이 정확하지 못할 경우 착지라인을 벗어나게 된다. 반대로 말하면 착지라인 안에 착지를 했다는 것은 기술 수행이 완벽했음을 의미한다. 앞서 설명했듯이 올림픽 등에 출전하는 선수들은 세계정상급 선수들이기 때문에 기술의 완성도는 높다 할 수 있다. 따라서 같은 조건일 경우 추가감점의 여부가 메달획득에 영향을 미친다고 할 수 있다. 그러나 이 연구에서는 추가감점 범위를 고려하지 않고 추가감점의 여부만을 고려했다는 점에서 제한이 따른다. 또한 경기결과 수가 제한적이고 아시안게임, 세계선수권대회, 올림픽 등 대회에 대한 가중치가 다르기 때문에 대회 가중치에 따라 결과는 달라질 수 있다. 이 연구결과에서 산출한 결승진출 가능성 높은 선수의 특성과 메달획득 모형을 확고히 하기 위해서는 반복적인 후속연구를 통해 다수의 증거가 요구됨을 밝혀둔다. 그럼에도 불구하고 종합적인 관점에서 메달획득을 위한 최적모형을 탐색하여 메달획득을 위한 기초자료를 제공할 수 있었다는 점에서 그 가치가 적지 않다.
향후 연구에서는 보다 많은 경기결과에 대한 분석을 통하여 메달획득을 위한 최적의 모형을 찾아낼 수 있는 연구가 지속되기를 희망한다.
이 연구는 남자 기계체조 도마경기 메달 획득을 위한 최적모형을 탐색하는 것이 목적이었다. 구체적으로는 의사결정나무분석을 활용하여 도마종목 결승진출 가능성 높은 선수의 특성 및 도마결승경기 메달획득조건을 탐색하여 도마경기 경기력 향상을 위한 기초자료를 제공하는 것이다. 이 목적을 달성하기 위하여 2012년 런던올림픽 이후 새로운 규정이 도입된 2013년부터 2016년까지의 국제체조연맹이 주관한 공식대회 다섯 경기에 대한 자료를 수집하였다. 국적, 및 경기정보에 대한 전체 다섯 개의 예측변수를 토대로 의사결정나무 분석을 적용하여 메달획득을 위한 최적모형을 확인하였다. 이 연구의 결론은 다음과 같다. 첫째, 도마종목 결승진출 가능성 높은 선수의 특성 및 메달획득을 위한 최적 변수는 난도점수인 것으로 확인되었다. 둘째, 도마종목 결승진출 가능성 높은 선수의 특성은 난도점수가 5.6점 보다 크고 실행점수가 8.6점 이상일 때 결승에 진출할 확률이 81.2%이다. 셋째, 메달획득을 위한 최적모형은 난도점수가 6.0점 보다 크고 추가감점이 없을 때 메달을 획득할 확률이 86.7%이다. 이 연구결과는 기계체조 도마경기의 메달획득을 위한 전략을 수립하기 위한 기초자료로 활용될 수 있을 것으로 판단한다.